Chapitre 3 Calcul des déperditions

Pour une zone thermique, ou pour un bâtiment monozone (c’est-à-dire dont on suppose la température intérieure uniforme), on définit un coefficient de déperdition $D$ (W.K$^{-1}$) comme le rapport entre la puissance de chauffage ou de refroidissement $\Phi$ (qui inclut les apports de chaleur solaires ou internes), et l’écart de température intérieur-extérieur en conditions stationnaires :

\[\begin{equation} \Phi = D \left(T_i - T_e\right) \tag{3.1} \end{equation}\]

(note: en été, si $T_i < T_e$, la puissance $\Phi$ est négative)

Le but de ce chapitre est d’exprimer $D$ en fonction des caractéristiques du bâtiment.

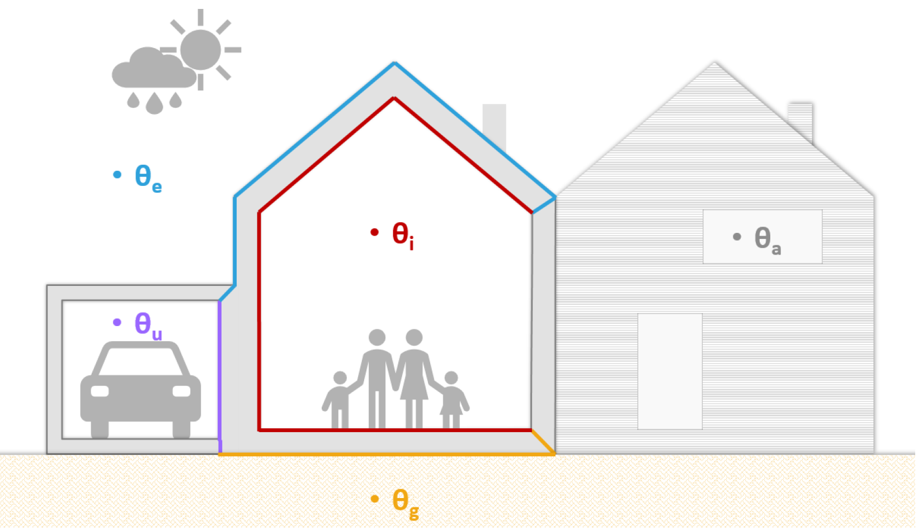
Echanges thermiques entre zones à des températures différentes: local chauffé $T_i$, extérieur $T_e$, local adjacent $T_a$, local non chauffé $T_u$, sol $T_g$

Figure 3.1: Echanges thermiques entre zones à des températures différentes: local chauffé $T_i$, extérieur $T_e$, local adjacent $T_a$, local non chauffé $T_u$, sol $T_g$

Les déperditions thermiques sont la conséquence d’une différence de température entre la zone chauffée et les milieux qui l’entourent : ambiance extérieure, zones adjacentes chauffées ou non, sol.

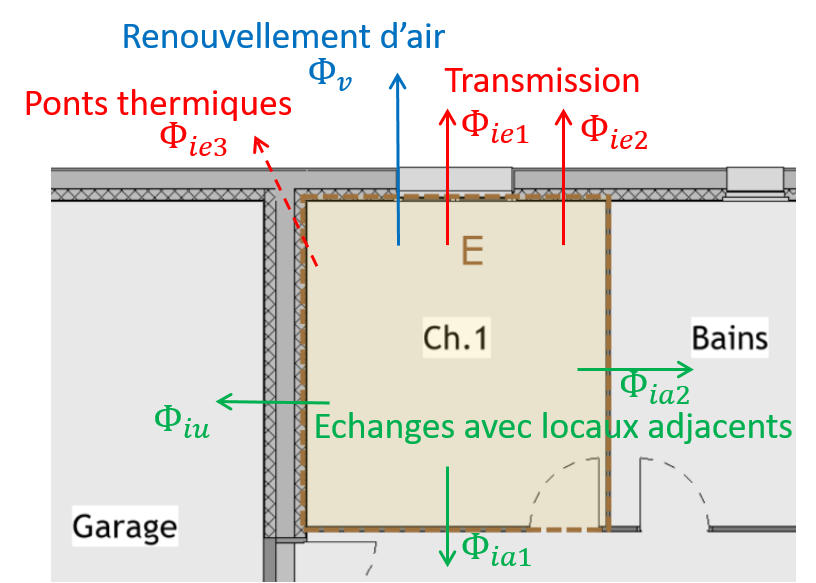
Figure 3.2: Illustration de flux déperditifs

Le flux total $\Phi$ est la somme des flux à travers chaque composant de la surface déperditive.

Flux par transmission (conduction et convection) à travers les parois planes et fenêtres,
Flux convectif dû au renouvellement d’air (ventilation, infiltrations),
Ponts thermiques,
Echanges avec les locaux adjacents, chauffés ou non, et le sol.

Chacun de ces flux est proportionnel à l’écart de température entre les deux milieux. Dans l’exemple de la figure 3.2, un des flux par transmission entre l’intérieur et l’extérieur est dénoté ainsi :

\[\begin{equation} \Phi_{ie1} = H_1 \left(T_i - T_e\right) \end{equation}\]

où $H_1$ est le coefficient de déperdition par transmission d’un des composants de la paroi (par exemple la fenêtre sur cette figure).

Chacune des sections suivantes détaille le calcul des différents flux, et on fait le bilan de ces déperditions en section 3.5 pour le calcul du coefficient global $D$ ou de son équivalent $U_\mathit{bat}$.

3.1 Transmission dans une paroi plane

Résumé en vidéo :

3.1.1 Conduction 1D et analogie électrique

La conduction thermique est décrite par la loi de Fourier : la densité de flux de chaleur $\phi$ (W.m$^{-2}$) est proportionnelle au gradient de température.

\[\begin{align} \rho c_p \frac{\partial T}{\partial t} & = -\vec{\nabla} \cdot \vec{\varphi} \tag{3.2} \\ \vec{\varphi} & = - \lambda \vec{\nabla} T \tag{3.3} \end{align}\]

Dans le cas général, $\vec{\phi}$ est un vecteur. Dans le cas unidimensionnel on le considère ici comme un scalaire, qui peut prendre des valeurs négatives. La conduction 1D le long d’une direction $x$ se formule :

\[\begin{align} \rho c_p \frac{\partial T}{\partial t} & = \lambda \frac{\partial^2 T}{\partial x^2} \tag{3.4} \\ \varphi & = - \lambda \frac{\partial T}{\partial x} \tag{3.5} \end{align}\]

Si on suppose de plus que le transfert est stationnaire, où toutes les grandeurs sont constantes dans le temps, l’équation (3.4) devient :

\[\begin{equation} \frac{\partial^2T}{\partial x^2} = 0 \tag{3.6} \end{equation}\]

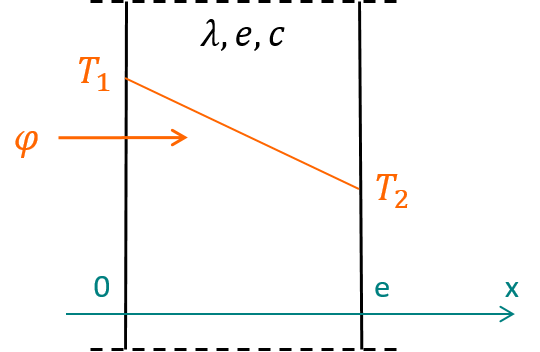
Figure 3.3: Conduction 1D stationnaire dans un solide

Sous ces deux hypothèses (transfert 1D et stationnaire), la dérivée seconde de la température sur la direction $x$ est donc nulle. En intégrant deux fois l’équation (3.6), on en déduit que le profil de température à travers un solide est linéaire entre ses deux conditions aux limites, comme montré sur la figure 3.3 :

\[\begin{equation} T(x) = T_1 + \frac{x}{e} \left(T_2-T_1\right) \tag{3.7} \end{equation}\]

De plus, si on inclut cette expression dans l’équation (3.5), on obtient :

\[\begin{equation} \varphi = - \lambda \frac{\partial T}{\partial x} = \frac{\lambda}{e} \left(T_1-T_2\right) \tag{3.8} \end{equation}\]

Le flux de chaleur $\varphi$ est donc proportionnel à l’écart de température de part et d’autre du mur. On appelle résistance thermique $R$ (m$^2$.K.W$^{-1}$) le rapport entre l’épaisseur du mur $e$ et sa conductivité thermique $\lambda$, et on appelle conductivité thermique $U$ (W.m$^{-2}.$K$^{-1}$) l’inverse de la résistance :

\[\begin{align} R & = \frac{e}{\lambda} \tag{3.9} \\ U & = \frac{1}{R} = \frac{\lambda}{e} \tag{3.10} \\ \varphi & = U \, \Delta T = \frac{\Delta T}{R} \tag{3.11} \end{align}\]

L’équation (3.11) est équivalente à la loi d’Ohm utilisée en électricité, où les températures sont les potentiels aux noeuds du circuit, et le flux de chaleur $\varphi$ est l’intensité traversant la résistance $R$.

Figure 3.4: Résistance thermique

Table 3.1: Exemples de propriétés thermiques de quelques matériaux
Matériau	Béton	Isolant	Plâtre	Acier
$\lambda$ (W.m$^{-1}.$K$^{-1}$)	1,75	0,04	0,35	1,1
$\rho$ (kg.m$^{-3})	2300	50-100	800	2500
$c_p$ (J.kg$^{-1}.$K$^{-1}$)	1000	1030	1000	750

Le flux de chaleur surfacique $\varphi$ a pour dimension (W.m$^{-2}$) : il est ramené par unité de surface du mur. La chaleur totale $\Phi$ (W) traversant un mur de surface $S$ est simplement :

\[\begin{equation} \Phi = S . \varphi = S . U . \Delta T \tag{3.12} \end{equation}\]

où on peut noter $H = S . U$ (W.K$^{-1}$) le coefficient de déperdition total de cet élément.

3.1.2 Assemblage de résistances

L’avantage de l’analogie électrique est qu’elle permet facilement de représenter les transferts à travers des murs composés de plusieurs couches de matériaux, ou des parois composées de plusieurs composants (partie opaque et fenêtres).

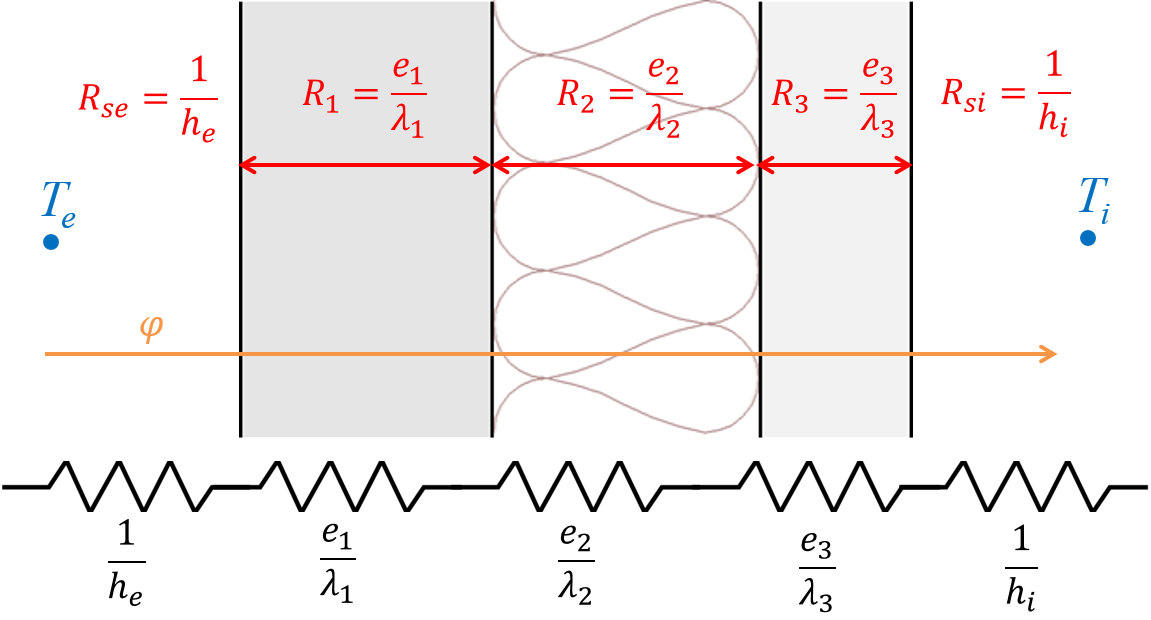
Figure 3.5: Addition des résistances thermiques en série

Les résistances s’additionnent en série : lorsqu’un mur est composé de plusieurs couches (isolant, mur porteur, enduit…) comme sur la figure 3.5, sa résistance thermique totale est la somme des résistances de chaque couche.

\[\begin{equation} R = \sum_i R_i = \sum_i \dfrac{e_i}{\lambda_i} + R_{se} + R_{si} \tag{3.13} \end{equation}\]

Cette expression inclut deux résistances de transfert surfaciques $R_{se}$ et $R_{si}$ qui seront expliquées plus bas (section 3.1.3).

La conductivité thermique totale du mur $U$ (W.m$^{-2}.$K$^{-1}$) est alors l’inverse de cette résistance totale :

\[\begin{align} U = \frac{1}{R} = \frac{1}{\sum_i \dfrac{e_i}{\lambda_i} + R_{se} + R_{si}} \tag{3.14} \end{align}\]

Attention : cette conductivité totale n’est pas la somme des conductivités de chaque couche. Ce sont les résistances qui s’additionnent en parallèle, et $U$ est l’inverse de cette somme.

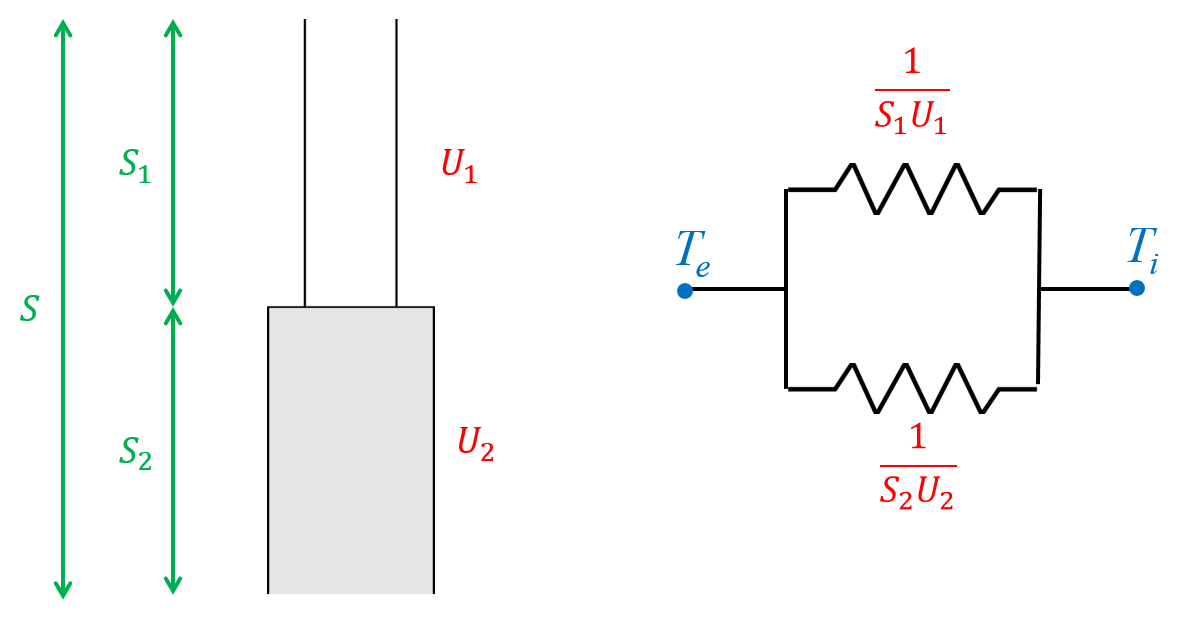
Figure 3.6: Addition des conductances thermiques en parallèle

A l’inverse, lorsqu’un mur est composé de plusieurs éléments séparés (paroi opaque, vitrage…), le flux de chaleur traverse plusieurs résistance en parallèle (figure 3.6). La conductance totale $H$ (W/K) de ce mur est alors la somme des conductances de chaque élément.

\[\begin{equation} H = U_\mathit{total} \, S_\mathit{total} = \sum_i U_i \, S_i \tag{3.15} \end{equation}\]

Attention : ce ne sont pas les coefficients $U$ (W.m$^{-2}$.K$^{-1}$) qui s’additionnent en parallèle, mais les conductances, c’est-à-dire les produits des $U$ avec les surfaces $S$ de chaque composant.

Enfin, dans le cas d’un mur plus complexe où plusieurs composants séparés sont chacun composés de plusieurs couches, il faut procéder dans l’ordre :

Calculer la résistance totale $R$ (en série) de chaque composant puis son coefficient $U$
Additionner les conductances $U.S$ de chaque composant pour obtenir la conductance de l’ensemble.

Table 3.2: Trois coefficients similaires pour décrire la performance thermique d’une paroi
Variable	Nom	Unité
$R$	Résistance thermique	m$^2$.K.W$^{-1}$
$U$	Coefficient de transfert	W.m$^{-2}.$K$^{-1}$
$H$	Coefficient de déperdition	W.K$^{-1}$

3.1.3 Résistances superficielles

On a vu que sur la figure 3.5 qu’une résistance thermique était placée entre la surface de la paroi et la température de l’air. Elle est égale à l’inverse du coefficient de convection $h$ (même dimension W.m$^{-2}.$K$^{-1}$ qu’un coefficient $U$) qui quantifie la convection à l’interface.

Figure 3.7: Coefficient de transfert $h$ et résistance surfacique $R_s$

La valeur de $h$ est surtout fonction de la vitesse d’air le long de la paroi. Sur la façade extérieure, le vent augmente les échanges convectifs entre l’air et la surface : le coefficient $h$ sera plus élevé donc la résistance surfacique plus faible, et donc l’écart entre les températures de l’air et de la surface est plus faible également.

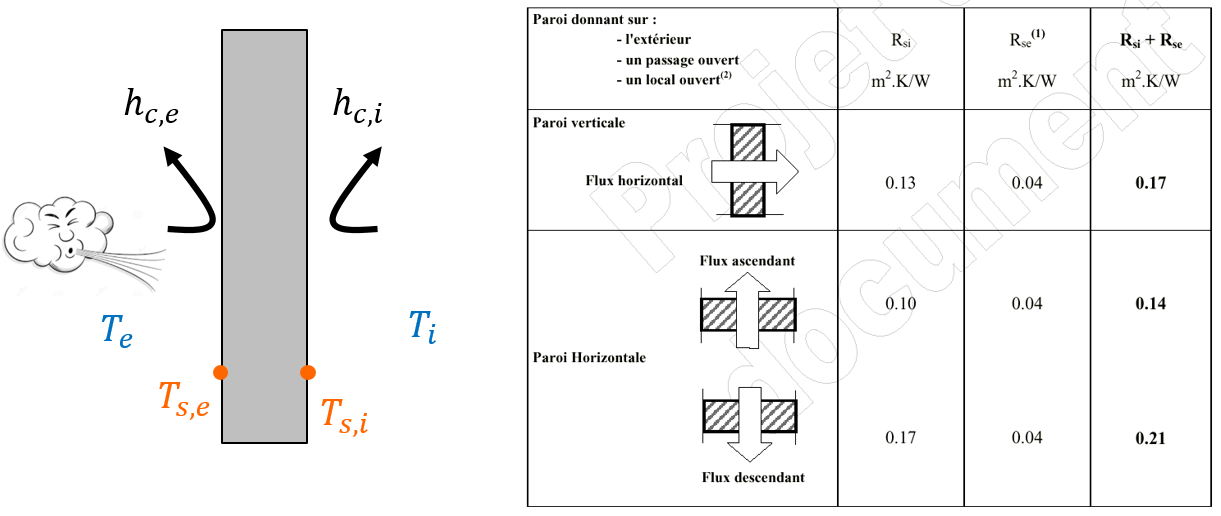
Figure 3.8: Quelques valeurs réglementaires de résistances surfaciques issues des règles Th-Bat 2020

3.1.4 Menuiseries

Figure 3.9: Conductance des fenêtres

Pour les fenêtres, trois conductances sont définies (selon les normes ISO 10077-1 et ISO 10077-2) :

Coefficient $U_g$ : conductance du vitrage (glass)
Coefficient $U_f$ : conductance du cadre (frame)
Coefficient $U_w$ : conductance de la fenêtre entière (window)

Généralement, les valeurs des coefficients $U_g$, $U_f$, $U_w$ sont calculées par les fabricants et renseignées dans les spécifications techniques des produits. La base de données EDIBATEC, qui est très utilisée lors des calculs réglementaires, contient un grand nombre de données fabriquant.

3.2 Ponts thermiques

Un pont thermique est une zone ponctuelle ou linéaire qui, dans l’enveloppe d’un bâtiment, présente une variation de résistance thermique : liaisons entre une menuiserie et une paroi opaque, planchers intermédiaires, murs de refend, seuil de porte…

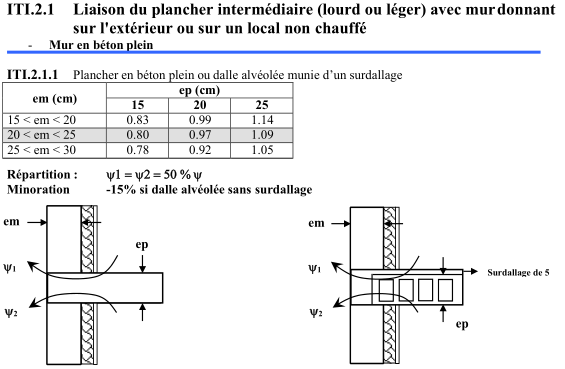
Figure 3.10: Exemple de règle Th-bat donnant le coefficient de transmission d’un pont thermique

Les règles Th-Bat 2020 traitent de manière différente les ponts thermiques structurels et les ponts thermiques intégrés.

Les ponts thermiques structurels sont les ponts thermiques situés à la jonction entre des éléments de parois.
Les ponts thermiques intégrés sont des ponts thermiques répartis de manière régulière sur toute la surface des parois : montants des ossatures bois, rails de maintien des parements, etc.

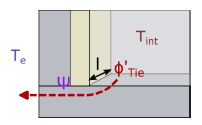
Figure 3.11: Pont thermique linéique

Le flux au travers d’un pont thermique linéique séparant deux zones aux températures $T_i$ et $T_e$ s’exprime : \[\begin{equation} \Phi_{pt} = l \cdot \psi \cdot (T_i-T_e) \tag{3.16} \end{equation}\]

où $l$ est la longueur du pont thermique et $\psi$ son coefficient en (W.m$^{-1}$.K$^{-1}$) qui dépend de sa nature.

Les valeurs de coefficient $\psi$ ont été obtenues à l’aide de simulations numériques dans un grand nombre de configurations courantes, afin de constituer des catalogues de valeurs. Ceux-ci sont disponibles dans les règles Th-Bat.

3.3 Echanges convectifs

Les transferts d’air entre l’intérieur et l’extérieur, ou entre différentes zones, entraînent un transfert de chaleur par convection. L’air entrant dans une pièce doit être inclus dans son bilan thermique sous la forme d’un flux thermique sortant $\Phi_v$:

\[\begin{equation} \Phi_v = \dot{m} \, c_a \, (T_e-T_i) \tag{3.17} \end{equation}\]

où $\dot{m}$ est le débit entrant à la température $T_e$ dans la pièce $T_i$, et $c_a$ est la chaleur massique de l’air. Le terme $\dot{m} \, c_a$ a pour dimension (W/K) et peut être assimilé à un coefficient de déperditions.

Le débit d’air $Q_v$ est souvent exprimé en m$^3$/h. Quand c’est le cas, l’équation (3.17) peut se réécrire :

\[\begin{align} \Phi_v & = \rho \, c_a \, \frac{Q_v}{3600} \, (T_e-T_i) \tag{3.18} \\ & = 0.34 \, Q_v \, (T_e-T_i) \tag{3.19} \end{align}\]

Les débits de renouvellement d’air dans les locaux peuvent résulter de trois composantes :

La ventilation mécanique contrôlée (VMC) qui peut imposer un débit d’air neuf réglementaire,
Les infiltrations à travers les défauts d’étanchéité de l’enveloppe,
La ventilation naturelle sous l’effet du vent et du tirage thermique

Le calcul des débits d’air est l’objet du chapitre 4.

3.4 Locaux non chauffés

Souvent, une pièce chauffée (ou climatisée) est adjacente à un local non chauffé (ou non climatisé) à la température $T_u$ : garage, combles, hall…

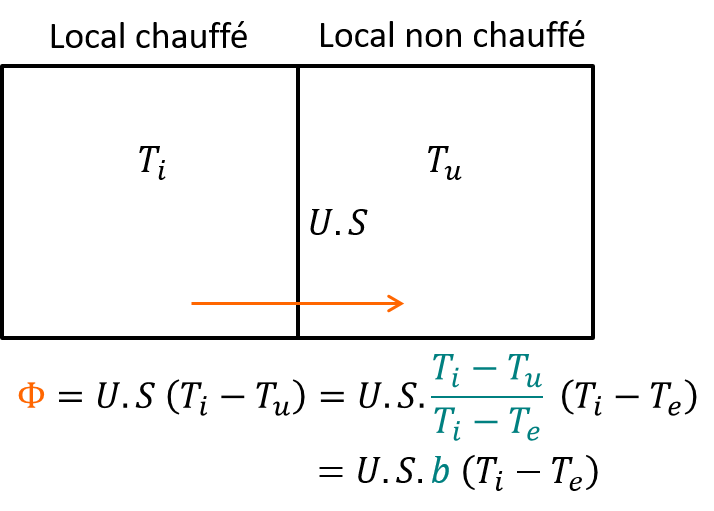
Figure 3.12: Déperditions entre un local dont la température est contrôlée et un où elle ne l’est pas

Afin de toujours formuler les déperditions thermiques de la pièce chauffée comme proportionnelles à l’écart de température intérieur-extérieur, on définit un coefficient de réduction de température $b$ comme indiqué sur la figure 3.12 :

\[\begin{equation} b = \frac{T_i-T_u}{T_i-T_e} \tag{3.20} \end{equation}\]

Ce coefficient permet d’écrire les déperditions de la pièce chauffée vers l’extérieur à travers le local non chauffé indépendamment de la température $T_u$ de celui-ci, mais selon le coefficient $U$ et la surface $S$ de la paroi qui les sépare :

\[\begin{equation} \Phi = U . S . b . (T_i - T_e) \tag{3.21} \end{equation}\]

On peut aussi démontrer que le coefficient $b$ s’exprime lui-même indépendamment de $T_u$, en fonction du coefficient de déperditions du local non chauffé vers l’extérieur $D_{ue}$, et celui de la séparation entre les deux locaux $D_{iu}$ :

\[\begin{equation} b = \frac{D_{ue}}{D_{ue}+D_{iu}} \tag{3.22} \end{equation}\]

3.5 Bilan des déperditions

On peut agréger toutes les déperditions décrites dans ce chapitre pour exprimer le coefficient global $D$ de la formule (3.1), qui représente la puissance thermique à dépenser par degré d’écart entre l’intérieur et l’extérieur, en conditions stationnaires.

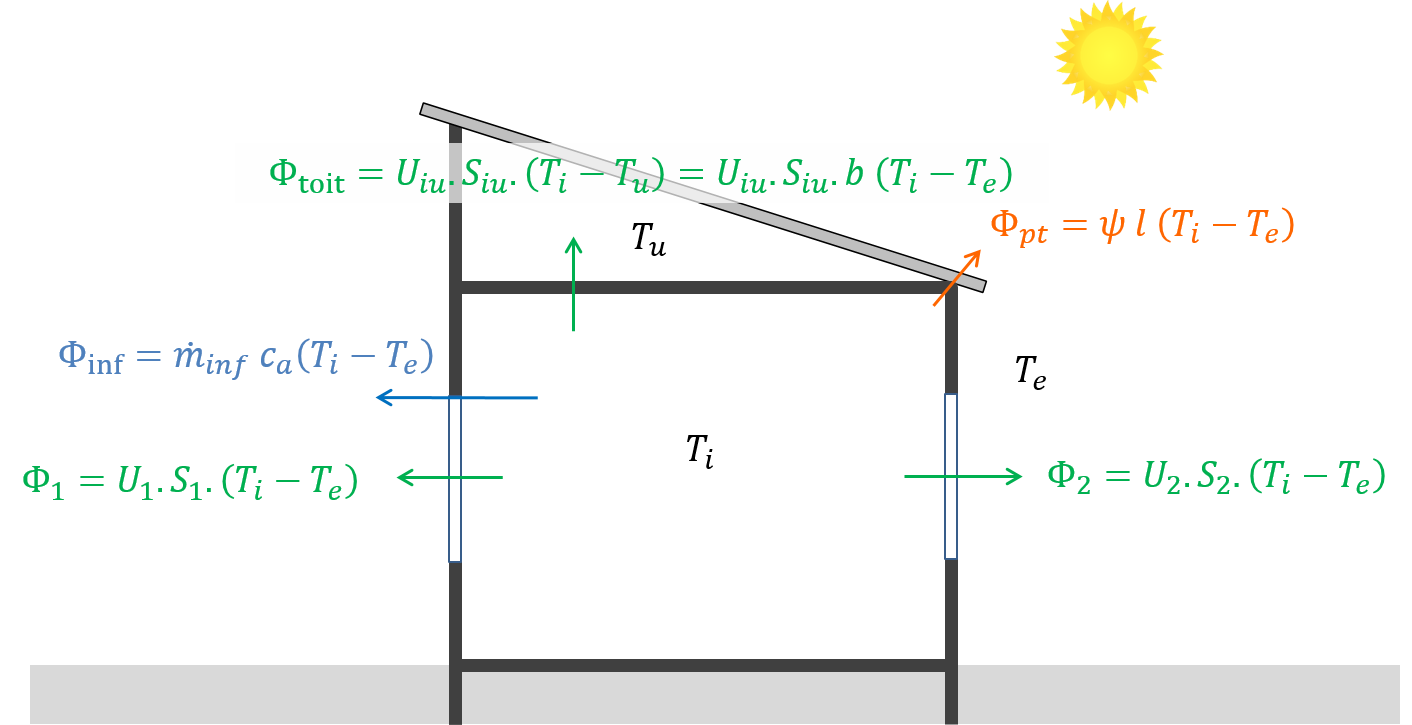
Figure 3.13: Exemple d’un bilan de déperditions

Le bilan des déperditions d’un local est l’inventaire des composants de sa surface déperditive. Il inclut :

Les déperditions par transmission à travers plusieurs parois planes ou fenêtres $\Phi_{tr} = \sum_j \, U_j \, S_j \, b_j \,(T_i - T_e)$
Les ponts thermiques $\Phi_{pt} = \sum_k \, l_k \, \psi_k \, b_k \, (T_i-T_e)$
Des déperditions dues au renouvellement d’air $\Phi_v = 0.34 \, Q_v \, (T_i - T_e)$

où les coefficients $b$ indiquent que chaque terme est susceptible de désigner des déperditions vers un local non chauffé, à une température différente de la température extérieure. Pour une paroi séparant directement la zone chauffée de l’air extérieur, $b=1$. Ces coefficients permettent d’écrire tous les termes du bilan proportionnellement au même écart de température intérieur-extérieur.

La somme des déperditions est donc dans cet exemple:

\[\begin{align} \Phi & = \sum_j \, U_j \, S_j \, b_j \, (T_i - T_e) + \sum_k \, l_k \, \psi_k \, b_k \, (T_i-T_e) + 0.34 \, Q_v \, (T_i - T_e) \tag{3.23} \\ & = D \, (T_i - T_e) \tag{3.24} \end{align}\]

Et le coefficient global de déperditions $D$ est donc, en (W/K):

\[\begin{equation} D = \sum_j \, U_j \, S_j \, b_j + \sum_k \, l_k \, \psi_k \, b_k + 0.34 \, Q_v \tag{3.25} \end{equation}\]

On utilise également le coefficient global de transmission surfacique $U_\mathit{bat}$ (W.m$^{-2}$.K$^{-1}$), qui est la conductance $D$ rapportée à la surface déperditive totale de l’enveloppe :

\[\begin{equation} U_\mathit{bat} = \frac{D}{\sum S} = \frac{\sum_j \, U_j \, S_j \, b_j + \sum_k \, l_k \, \psi_k \, b_k + 0.34 \, Q_v}{\sum_j S_j} \tag{3.26} \end{equation}\]

J’insiste une dernière fois sur un point : on n’obtient pas le $U_\mathit{bat}$ en additionnant les coefficients $U$ directement, mais avec une somme pondérée par les surfaces déperditives.

On a surtout parlé dans ce chapitre de déperditions thermiques, ce qui sous-entend que la chaleur sort du bâtiment donc que celui-ci est chauffé par rapport à l’extérieur. Tous ces calculs sont cependant toujours valables en été, lorsque la chaleur rentre dans le bâtiment car le rapport des températures s’inverse. On peut alors utiliser les mêmes formules, qui donneront un résultat négatif (apports de chaleur = déperditions négatives).

3.6 Exercices

3.6.1 Ex 1 : déperditions d’une pièce

Enoncé

Les parois d’u’un local sont composées de :

44 m$^2$ de mur en béton ($e_c=15$ cm, $\lambda_c=2,3$ W/(m.K)) avec une couche d’isolant ($e_{i}=10$ cm, $\lambda_{i}=0.04$ W/(m.K))
8 m$^2$ de double vitrage ($U_v=3.3$ W/(m$^2$.K))
La résistance surfacique intérieure est $h_i = 0.11$ (m$^2$.K)/W, et la résistance extérieure est $h_e = 0.07$ (m$^2$.K)/W

Le local a également un taux de renouvellement d’air depuis l’extérieur de 9 m$^3$/h.

Quelle puissance doit-on fournir pour maintenir le local à 19°C, si la température extérieure est de 2°C ?

Solution

Les déperditions thermiques totales du local sont la somme de trois parties : les pertes par le mur béton+isolant, les pertes par les vitres et les pertes par renouvellement d’air. Il suffit de calculer ces trois parties et de les additionner.

1. Mur béton isolé

La résistance thermique totale doit tenir compte des deux couches du mur et des résistances surfaciques

$R_1 = h_i + \frac{e_b}{\lambda_b} + \frac{e_\mathit{iso}}{\lambda_\mathit{iso}} + h_e = 0,11 + \frac{0,15}{2,3} + \frac{0,10}{0,04} + 0,07 = 2,75$ (m$^2$.K)/W

La déperdition $D_1$ est ensuite l’inverse de cette résistance, multiplié par la surface de mur:

$D_1 = \frac{S_1}{R_1} = \frac{44}{2,75} = 16,03$ W/K

2. Vitres

Le coefficient $U_v$ fourni pour le vitrage n’inclut probablement pas les résistances surfaciques. Il faut les ajouter à la résistance de ce composant pour obtenir le coefficient de déperdition total des vitres $D_2$:

$D_2 = \frac{S_2}{h_i+\frac{1}{U_v}+h_e} = \frac{8}{0.11+\frac{1}{3,3}+0,07} = 16,56$ W/K

3. Renouvellement d’air

Si le débit d’air est donné en (m$^3$/h), le coefficient de déperdition qui y est associé se calcule facilement:

$D_3 = 0,34 \, Q_v = 3,06$ W/K

Total

La puissance totale $\Phi$ perdue par le local est la somme des trois composantes de déperditions, multipliée par l’écart de température intérieur-extérieur:

$\Phi = \underbrace{(D_1+D_2+D_3)}_{W/K}.\underbrace{\Delta T}_{K} = (16,03 + 16,56 + 3,06 ). (19-2) = 606$ W

3.6.2 Ex 2: bilan thermique de deux pièces

On considère un bâtiment composé de deux zones thermiques : la zone 1 est chauffée, la zone 2 est non chauffée. Un débit d’air passe de l’extérieur vers la zone 1 puis vers la zone 2. Les données du problèmes sont résumées ici :

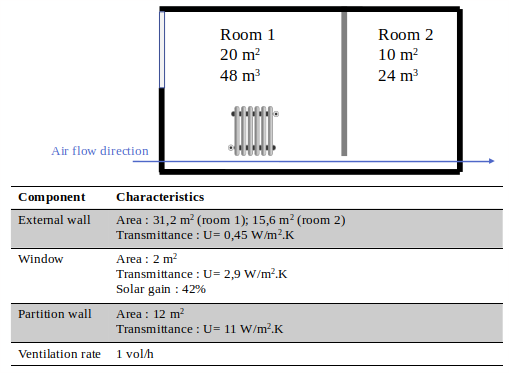
Figure 3.14: Exercice 2

Ecrire le bilan thermique de chaque pièce
Dimensionner l’équipement de chauffage permettant de maintenir une température de 19°C dans la pièce 1, pour une température extérieure moyenne de 9°C
Quelle est la solution si la direction du courant d’air est inversée ?

Matériau	Béton	Isolant	Plâtre	Acier
\(\lambda\) (W.m\(^{-1}.\)K\(^{-1}\))	1,75	0,04	0,35	1,1
\(\rho\) (kg.m$^{-3})	2300	50-100	800	2500
\(c_p\) (J.kg\(^{-1}.\)K\(^{-1}\))	1000	1030	1000	750

Variable	Nom	Unité
\(R\)	Résistance thermique	m\(^2\).K.W\(^{-1}\)
\(U\)	Coefficient de transfert	W.m\(^{-2}.\)K\(^{-1}\)
\(H\)	Coefficient de déperdition	W.K\(^{-1}\)