Chapitre 2 Bilan de chaleur et besoins

Ce chapitre sert d’introduction aux transferts thermiques et massiques qui seront approfondis dans les chapitres suivants de la partie I. Le but est de comprendre les phénomènes principaux de transferts, afin non seulement de comprendre le calcul réglementaire mais surtout de réaliser des calculs indépendamment de celui-ci.

2.1 Hypothèses et définitions

2.1.1 Locaux et parois

Pour le calcul énergétique réglementaire ou pour la simulation thermique, un bâtiment est découpé en zones, elles-mêmes découpées en groupes puis en locaux.

• Le niveau zone correspond à un regroupement des parties de bâtiment pour lesquelles les scénarios d’utilisation sont identiques.
• Le niveau groupe est l’échelle à laquelle sont calculées les températures intérieures, les degrés-heures d’inconfort et les besoins. Une zone peut être séparée en différents groupes si on doit en calculer séparément les températures ou les besoins.
• Le niveau local permet d’affiner les apports internes de chaleur et d’humidité dûs à l’occupation, dans plusieurs pièces au sein d’un même groupe.

Au contraire, le terme de zone est utilisé dans certains logiciels de simulation thermique pour désigner un espace où la température intérieure est supposée uniforme.

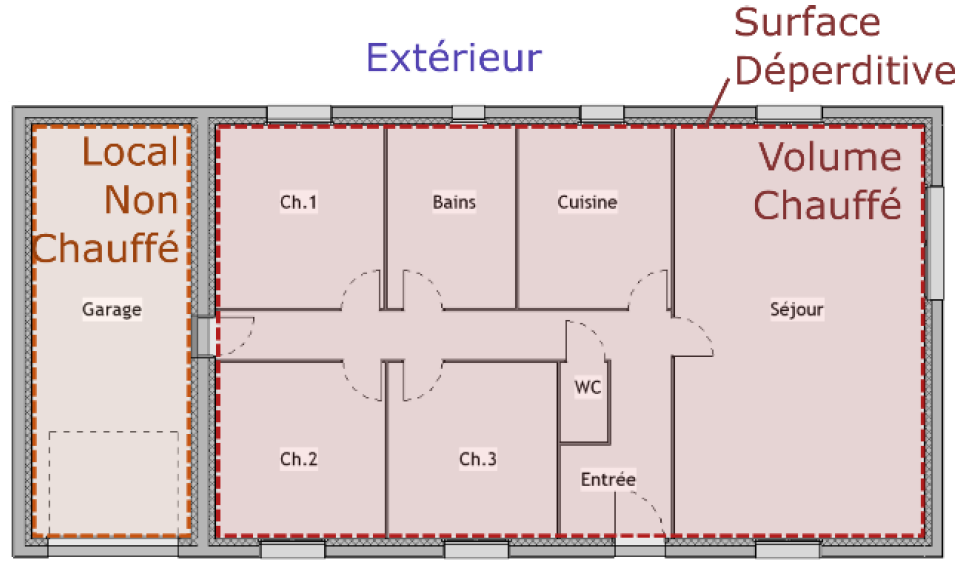
Figure 2.1: Quelques définitions

Le calcul des besoins de chauffage se basera sur un bilan de chaleur réalisé sur un volume chauffé (voir figure 2.1), composé d’un ou plusieurs locaux équipés d’un émetteur de chaleur. Un local non chauffé (LNC) est un local qui se situe entre le volume chauffé et le milieu extérieur, et qui n’est pas équipé d’un émetteur de chaleur (garage, comble perdu, véranda, vide sanitaire, etc.). Sa température résulte d’un équilibre entre la température des locaux chauffés et la température extérieure.

La surface déperditive est la surface qui sépare le volume chauffé du milieu extérieur et des LNC. Elle est composée des parois déperditives : murs, fenêtres, ponts thermiques.

2.1.2 Données d’entrée

La méthode de calcul repose sur des données d’entrée (affichées sur la figure 1.4. Certaines sont conventionnelles, fixées par la réglementation et non modifiables :

• Les données météorologiques (température et humidité, données solaires et d’éclairement, rayonnement froid vers la voûte céleste, précipitations, vitesse et direction du vent, température de base, température d’eau froide du réseau) sont définies par la zone climatique ;
• L’occupation : un scénario indique si chaque zone est occupée ou non, selon l’heure et le jour ;
• Les températures de consigne en chauffage et en refroidissement ;

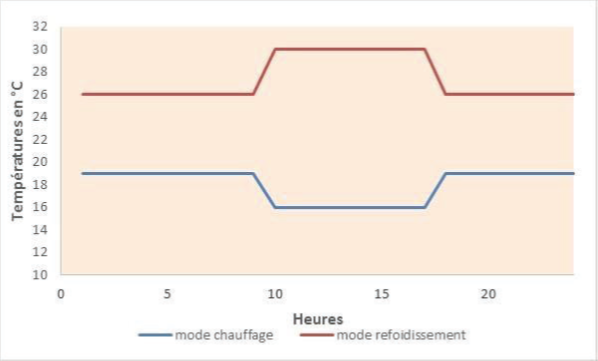
Figure 2.2: Exemple de températures de consigne en mode chauffage et refroidissement, pour une zone occupée ou non

• Les besoins de ventilation et d’éclairage ;
• Les besoins d’ECS ;
• Les scénarios de mobilité et d’usages spécifiques de l’énergie ;
• Les apports internes de chaleur et d’humidité liés à la présence humaine ou aux équipements. Ils sont définis au niveau des locaux.

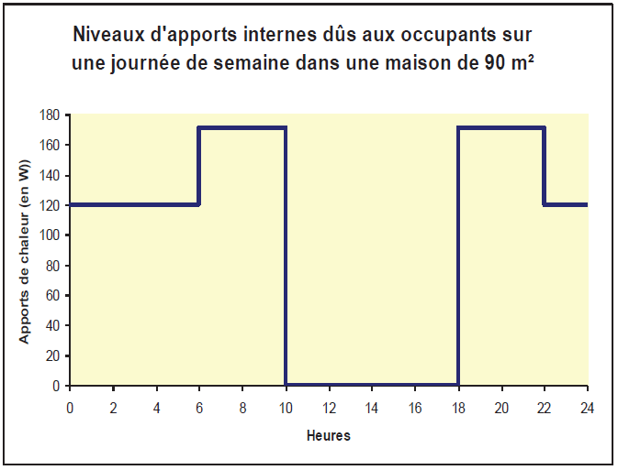
Figure 2.3: Exemple d’apports internes dûs aux occupants

Toutes ces données doivent être prises en compte pour le calcul des besoins du bâtiment en chauffage, refroidissement, éclairage et ECS.

2.2 Bilan thermique global

Le bilan de chaleur simplifié à l’échelle d’une zone thermique peut être résumé par l’équation suivante : la variation de l’énergie interne d’une zone est la différence entre le flux de chaleur entrant et le flux de chaleur sortant. \[\begin{equation} C \frac{\partial T_i}{\partial t} = \Phi_\mathit{CVC} + \Phi_\mathit{apports} - \Phi_\mathit{déperditions} \tag{2.1} \end{equation}\]

Le terme de gauche de l’équation comprend un terme de capacité thermique \(C\) [J/K] qui caractérise l’inertie thermique, c’est-à-dire la vitesse à laquelle la température va varier en conséquence d’un flux de chaleur entrant ou sortant. Le terme \(C \frac{\partial T_i}{\partial t}\) [W] est donc une variation d’énergie totale contenue dans la zone: la température varie s’il y a une différence entre ce qui rentre (\(\Phi_\mathit{CVC} + \Phi_\mathit{apports}\)) et ce qui sort (\(\Phi_\mathit{déperditions}\)).

Le terme \(\Phi_\mathit{CVC}\) est l’apport de chaleur par les systèmes de chauffage, ventilation et climatisation. Ce terme peut être négatif dans le cas du rafraîchissement (apport “négatif” de chaleur). Dans le cas particulier où on suppose que la température intérieure de la zone est constante, l’équation (2.1) peut se simplifier :

\[\begin{equation} \Phi_\mathit{CVC} = \Phi_\mathit{déperditions} - \Phi_\mathit{apports} \tag{2.2} \end{equation}\]

Cette formule simplifiée servira de base au calcul des besoins de chauffage et de refroidissement présentée plus bas.

Le terme \(\Phi_\mathit{apports}\) contient les apports de chaleur “gratuits” qui ne sont pas fournis par les systèmes CVC : apports solaires et apports internes divers (occupants, équipements, éclairage…). Pour le calcul des besoins, ceux-ci sont en général estimés à partir de scénarios conventionnels. L’exercice en fin de ce chapitre montre un exemple de calcul de ces apports gratuits.

Le terme \(\Phi_\mathit{déperditions}\) désigne les déperditions à travers les limites de la zone: enveloppe du bâtiment ou séparation avec les locaux non chauffés adjacents.

\[\begin{equation} \Phi_\mathit{déperditions} = D \left(T_i-T_e\right) \tag{2.3} \end{equation}\]

L’équation est écrite dans le sens de la chaleur quittant la zone, mais ses termes peuvent être négatifs par exemple si la température extérieure \(T_e\) est supérieure à celle de la zone \(T_i\) (déperditions “négatives”).

Le coefficient \(D\) de cette équation, en [W/K], est le coefficient global de déperditions thermiques de la surface déperditive de la zone. Il représente la quantité de chaleur à y fournir pour maintenir une différence de température de 1 K en conditions stationnaires. Il englobe les déperditions thermiques surfaciques à travers les parois, linéiques et ponctuelles au niveau des ponts thermiques, et celles dues aux infiltrations d’air.

Le calcul du coefficient de déperditions \(D\) d’un local est à lui seul l’objet du chapitre 3 car il agrège de nombreux termes de déperditions thermiques. Pour l’instant on le suppose connu pour le calcul des besoins.

2.3 Calcul des besoins

Le coefficient Bbio (voir 1.2.1) est basé sur les besoins de chauffage, refroidissement et d’éclairage artificiel à l’échelle d’un bâtiment entier. Ils sont déterminés en kWh/m\(^2\) et convertis en points selon cette formule : \[\begin{equation} \mathrm{Bbio} = 2 \cdot \mathrm{Bes}_\mathrm{chauffage} + 2 \cdot \mathrm{Bes}_\mathrm{froid} + 5 \cdot \mathrm{Bes}_\mathrm{eclairage} \tag{2.4} \end{equation}\]

Les besoins de chauffage et de refroidissement sont une quantité d’énergie, c’est-à-dire une puissance multipliée par un temps. 1 kWh est l’énergie consommée par un appareil d’une puissance de 1 kW fonctionnant pendant 1 heure. On peut donc calculer les besoins en intégrant l’équation (2.2) sur une certaine durée, par exemple 24 h :

\[\begin{align} \mathrm{Bes}_\mathit{chauffage} & = \int_{24h} \Phi_\textit{CVC} \, \mathrm{d}t \tag{2.5} \\ & = \int_{24h} D \left(T_i - T_e \right) \mathrm{d}t - \int_{24h} \Phi_\mathit{apports} \mathrm{d}t \tag{2.5} \end{align}\]

Les termes de cette équation sont des énergies, exprimées en général en [kWh].

Le premier terme de droite est l’intégrale des déperditions thermiques pendant 24 h, et dépend donc des températures intérieure \(T_i\) et extérieure \(T_e\) à chaque pas de temps. On simplifie ce terme grâce aux notions de degré-heure DH et de degré-jour DJ. Un degré-heure [K.h] est une différence de température entre intérieur et extérieur de 1 K pendant 1 h. Un degré-jour [K.jour] est la même chose pendant 1 jour.

\[\begin{align} \mathrm{Bes}_\mathit{chauffage} & = D \times \sum_{h=1}^{24} \underbrace{\left(T_i(h)-T_e(h)\right)}_{DH} - \mathrm{Apports} \tag{2.6} \\ & = D \times 24 \times \underbrace{\overline{\left(T_i-T_e\right)}}_{DJ} - \mathrm{Apports} \tag{2.7} \end{align}\]

Ces deux équations sont écrites pour calculer les besoins sur une journée en additionnant les écarts de températures heure par heure (équation (2.6)) ou en prenant la moyenne de cet écart en degrés-jours (équation (2.7)). On peut ensuite additionner cette moyenne quotidienne, jour après jour, pour estimer un besoin sur une plus longue période.

Par exemple, si, en moyenne de la journée, il fait 20°C à l’intérieur et 5°C degrés à l’extérieur, on parlera de 15 degrés-jours. De même 3 journées à 0°C extérieur seront comptabilisées comme 60 degrés-jours. Le coefficient 24 de l’équation (2.7) sert à convertir les degrés-jours en kWh.

Les DJ sont une donnée géographique : ils ne dépendent pas du bâtiment. C’est le coefficient de déperditions \(D\) qui caractérise l’isolation de chaque bâtiment, et donc ses besoins de chauffage et ses consommations.

Comme on peut le voir sur les équations (2.6) et (2.7), les besoins de chauffage en hiver sont réduits par la présence d’apports gratuits de chaleur dans le bâtiment : apports solaires et apports internes dûs aux occupants et tous leurs équipements. En été, ces apports augmentent le besoin de refroidissement.

Pour citer la réglementation concernant les logements : “conventionnellement, la puissance de chaleur dégagée par l’ensemble des équipements en occupation est prise égale à 5,7 W/m\(^2\), et en inoccupation égale à 1,1 W/m\(^2\).” Les autres catégories de bâtiments possèdent leurs propres scénarios d’apports internes de chaleur.

2.3.1 Les DJU

L’équation (2.7) montre que le besoin de chauffage moyen quotidien est la différence entre un terme proportionnel à l’écart de température intérieur-extérieur, et les apports. On peut la réécrire pour exprimer uniquement les besoins proportionnellement à un écart entre une température de référence \(T_\mathit{ref}\) et la température extérieure :

\[\begin{align} \mathrm{Bes}_\mathit{chauffage} & = D \times 24 \times \left(T_i-T_e\right) - \mathrm{Apports} \tag{2.8} \\ & = D \times 24 \times \left(T_\mathit{ref}-T_e\right) \tag{2.9} \end{align}\]

Où la température de référence est donc :

\[\begin{equation} T_\mathit{ref} = T_i - \frac{\mathrm{Apports}}{D \times 24} \tag{2.10} \end{equation}\]

Il s’agit de la température extérieure pour laquelle les besoins de chauffage sont nuls, c’est-à-dire où les apports de chaleur suffisent pour amener le local à la température \(T_i\) voulue. La différence \(\left(T_\mathit{ref}-T_e\right)\) est nommée degré jour unifié (DJU). Les DJU peuvent être utilisés pour un calcul très simplifiés en supposant une valeur connue de la température de référence. Cette hypothèse est cependant erronée car, comme on voit sur l’équation (2.10), \(T_\mathit{ref}\) dépend des apports (variables chaque jour et dans chaque bâtiment) et de la performance de chaque bâtiment \(D\) : un bâtiment bien isolé peut se passer de chauffage lorsque la température extérieure est de 10°C, alors qu’une passoire thermique aura besoin de chauffage à partir de 16 ou 17°C.

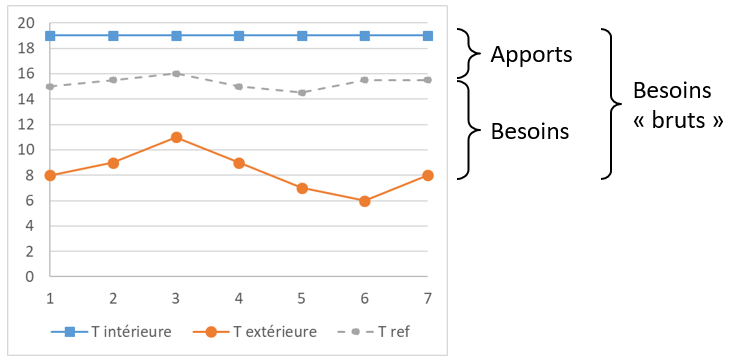
Figure 2.4: Besoins et apports en fonction des températures

La figure 2.4 illustre les différents termes de l’équation (2.8) sur une semaine. Les besoins bruts, ou totaux, de chauffage, sont les déperditions \(D \times 24 \times \left(T_i-T_e\right)\) proportionnelles à l’écart de température intérieur-extérieur. Ils sont satisfaits en partie par les apports gratuits, et en partie par la dépense réelle de chauffage \(\mathrm{Bes}_\mathit{chauffage} = D \times 24 \times \left(T_\mathit{ref}-T_e\right)\). La température de référence peut varier chaque jour, selon les conditions d’ensoleillement ou d’occupation.

2.3.2 Détail des transferts thermiques

La suite de la partie I du livre reste centrée sur les notations du calcul réglementaire, mais va aussi présenter les phénomènes de transfert plus en détail. Un des objectifs principaux est de comprendre les règles Th-Bat qui déterminent le coefficient \(D\).

Pour formuler les transferts thermiques (et massiques), on discrétise le bâtiment en un nombre fini de points dont on peut calculer la température.

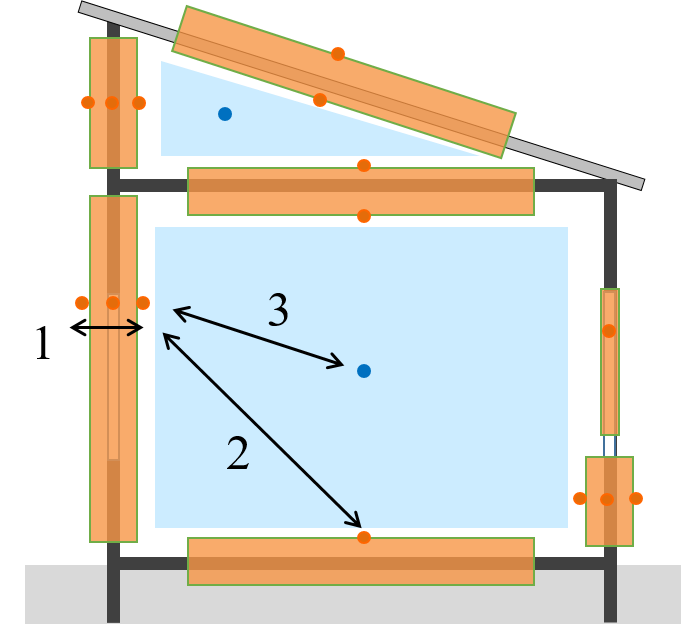
Figure 2.5: Discrétisation des températures dans un bâtiment: températures de surface ou interne aux parois (orange), et températures des zones d’air (bleu)

Les chapitres suivants vont détailler les trois types d’échange représentés sur la figure 2.5:

1. Conduction à travers les composants de l’enveloppe : chapitre 3 ;
2. Echanges radiatifs directs entre parois, déterminants pour estimer le confort thermique : chapitre 5 ;
3. Entre les parois et l’air de la pièce ;
4. Par convection due au déplacement d’air entre les zones : chapitre 4 ;

Par ailleurs, le chapitre 6 aborde les transferts thermiques en mode transitoire pour décrire les effets d’inertie thermique.

2.4 Exercices

2.4.1 Exercice 1 : calcul des DJU et des besoins

On reprend les données montrées sur la figure 2.4, où sont affichées les trois températures (intérieure, extérieure, référence) pendant une semaine.

Jour	T intérieure	T extérieure	T ref
1	19	8	15
2	19	9	15,5
3	19	11	16
4	19	9	15
5	19	7	14,5
6	19	6	15,5
7	19	8	15,5

• Calculer les besoins de chauffage (kWh) sur une semaine d’une maison de coefficient \(D=100\) W/K
• Sur une journée, les apports gratuits moyens sont de 14 kWh : quelle est la température de base ?

2.4.2 Exercice 2 : apports et besoins

On s’intéresse à 4 bâtiments dont on veut calculer les besoins de chauffage.

Bâtiment	Type	Ville	Déperditions (W/m2K)	Surface (m2)	Occupants
1	Logement collectif	Bordeaux	2	900	24
2	Maison individuelle	Chambéry	3,5	160	3
3	Bureaux	Marseille	2	1400	Voir tableau
4	Ecole primaire	Brest	0,625	600	Voir tableau

On calcule d’abord les apports de chaleur gratuits pendant la saison de chauffe. On suppose que cette saison dure 5 mois. Pour chaque bâtiment :

• Calculer les apports internes de chaleur moyens liés aux équipements en kWh/jour, puis la valeur totale pendant les 5 mois que dure la saison de chauffage.
• Calculer les apports internes liés aux occupants en supposant : 1 occupant = 2,5 kWh/jour
• On suppose que chaque bâtiment a une surface vitrée égale à 10% de sa surface de plancher, répartie également sur toutes les orientations. Calculer les apports solaires journaliers en kWh/jour en moyenne annuelle. Calculer ces apports pendant la saison de chauffe en supposant qu’elle contient 25% des apports solaires totaux.

En déduire le total des apports pendant les 5 mois de chauffage, et le besoin de chauffage en fonction des DJU (formule (2.7)).

Toutes les données nécessaires au calcul sont fournies ci-dessous.

Figure 2.6: Températures de base pour le dimensionnement, et degrés-jours annuels, pour chaque zone climatique de France métropolitaine

Figure 2.7: Apports solaires journaliers en kWh/jour à travers 1 m2 de vitrage vertical

Figure 2.8: Scénarios d’occupation et d’apports internes liés aux équipements