Chapitre 4 Renouvellement d’air

Les transferts de chaleur par renouvellement d’air ont été évoqués au chapitre précédent en raison du flux de chaleur \(\Phi_v\) (W) dans le bilan thermique d’un local sous l’effet d’un débit de renouvellement d’air \(Q_v\) (m\(^3\)/h): \[\begin{align} \Phi_v = 0.34 \, Q_v \, (T_e-T_i) \tag{4.1} \end{align}\]

Tout débit d’air entrant représente donc une déperdition thermique en hiver (\(T_e < T_i\)) ou un apport de chaleur supplémentaire en été (\(T_e > T_i\)). Un moyen de réduire les déperditions thermiques liées au renouvellement d’air est l’usage d’une VMC double flux ou d’une centrale de traitement d’air qui fournit aux locaux un air neuf préchauffé (ou refroidi, selon la saison), plutôt qu’à la température extérieure \(T_e\).

Les débits de renouvellement d’air dans les locaux peuvent résulter de trois composantes :

• La ventilation mécanique contrôlée (VMC) qui peut imposer un débit d’air neuf réglementaire,
• Les infiltrations à travers les défauts d’étanchéité de l’enveloppe,
• La ventilation naturelle sous l’effet du vent et du tirage thermique.

Les calculs détaillés de la norme EN 12831-1 prennent en compte les trois composantes du renouvellement d’air pour estimer les déperditions dus à la ventilation. Un même local peut recevoir plusieurs débits d’air entrant à des températures différentes.

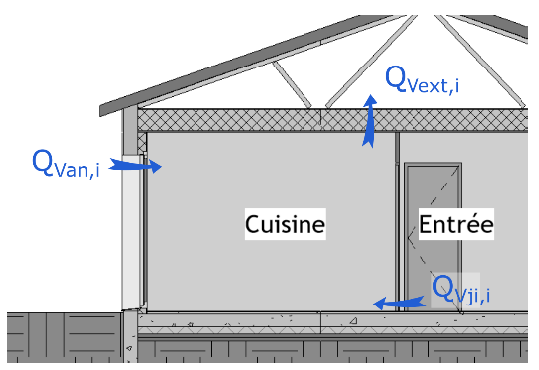
Figure 4.1: Bilan de masse d’air dans un local

Le bilan de masse d’air dans un local est très simple en principe : la somme des débits entrants est égale à la somme des débits sortants.

\[\begin{equation} \sum_i Q_{V,\mathit{in},i} = \sum_j Q_{V,\mathit{out},j} \tag{4.2} \end{equation}\]

4.1 Débits d’air neuf entrant

Une zone ventilée est un ensemble de pièces dont le renouvellement d’air est assuré par un unique système de ventilation. Généralement, un logement correspond à une zone ventilée. Dans une zone ventilée, le débit total d’apport d’air neuf \(Q_{Van}\) et le débit total d’air extrait \(Q_{Vext}\) sont calculés en sommant les débits correspondant dans les différents locaux :

\[\begin{align} Q_{Van} & = \sum_i Q_{Van,i} \tag{4.3} \\ Q_{Vext} & = \sum_i Q_{Vext,i} \tag{4.4} \end{align}\]

Les débits d’air neuf \(Q_{Van,i}\) ou extrait \(Q_{Vext,i}\) de chaque pièce sont imposés par la réglementation selon le type de bâtiment et son occupation. Lorsqu’un débit total d’air neuf \(Q_{Van}\) à l’échelle de toute la zone ventilée est imposé, on peut le répartir au prorata des volumes des locaux \(V_i\) :

\[\begin{equation} Q_{Van,i} = \frac{V_i}{\sum_i V_i} Q_{Van} \tag{4.5} \end{equation}\]

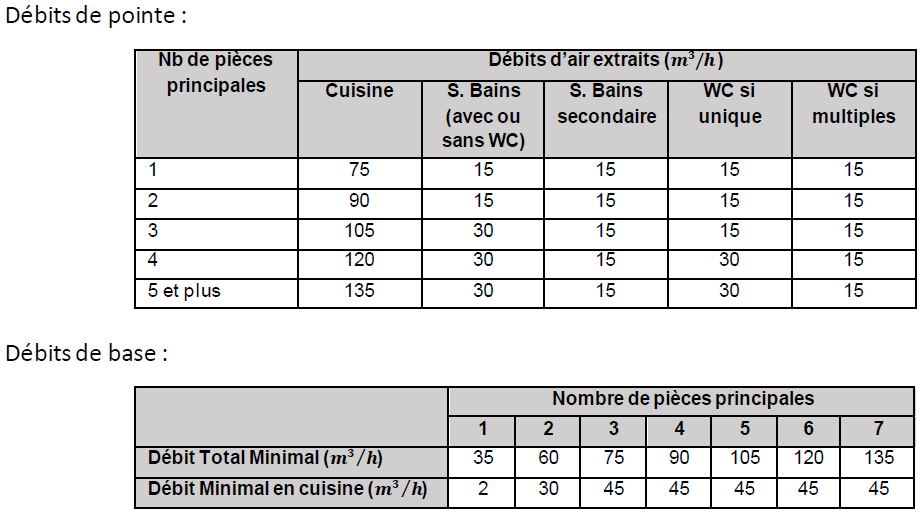
Figure 4.2: Débits d’extraction minimums imposés dans les bâtiments d’habitation neufs

Dans les bâtiments d’habitation, la réglementation fixe deux niveaux de débits pour les systèmes autoréglables : le débit de base \(\left(Q_{Vext}\right)_B\), et le débit de pointe \(\left(Q_{Vext}\right)_P\). Le débit de pointe est censé assurer un renouvellement d’air suffisant lorsque les activités des occupants génèrent beaucoup de polluants (douches, cuisine, etc.). Le débit de base assure un renouvellement d’air suffisant le reste du temps. Les débits de ventilation dans les bâtiments autres que les bâtiments d’habitation sont fixés par le Code du Travail.

4.2 Perméabilité à l’air des bâtiments

La mesure de la perméabilité à l’air des bâtiments neufs a été rendue obligatoire avec la RT2012. Elle est réalisée une fois le bâtiment terminé. Elle vise essentiellement à vérifier la qualité de la mise en oeuvre du bâtiment (joints autour des fenêtres, continuité du pare-vapeur, absences de fissures dans les maçonneries, etc.).

La mesure de perméabilité se fait avec un test de la porte soufflante. L’intérieur du bâtiment (ou du logement si immeuble de logement collectif) est mis en dépression (ou en surpression, le test peut se faire dans les deux sens), pour induire un écoulement au travers des éventuels défauts d’étanchéité de l’enveloppe (flèches vertes dans le schéma ci-dessous). Le test se fait après avoir colmaté toutes les ouvertures volontaires vers l’extérieur (bouches de soufflage et d’extraction, entrée d’air situées dans les menuiseries).

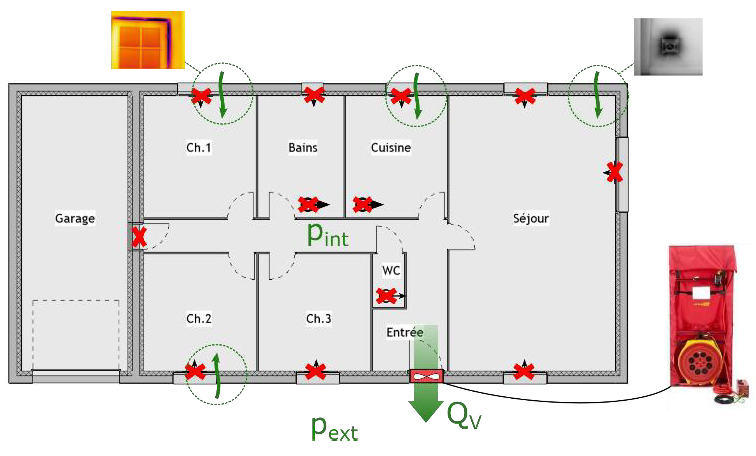
Figure 4.3: Porte soufflante

La porte soufflante est constituée d’une bâche étanche maintenue par un cadre qui s’adapte au cadre de la porte d’entrée du bâtiment testé, et d’un ventilateur. Lorsque le ventilateur est en route, le dispositif mesure simultanément le débit volumique \(Q_v\) qui passe au travers du ventilateur (et donc au travers des défauts d’étanchéité), et la différence de pression entre l’intérieur et l’extérieur du bâtiment \(\Delta p = \left| p_\mathit{in} - p_\mathit{ext} \right|\).

A l’issue d’un test et de plusieurs points de mesure, le graphique \(Q_v(\Delta p)\) est tracé, et permet de trouver les coefficients \(K\) et \(n\) d’une relation entre les deux grandeurs de la forme : \[\begin{equation} Q_v = K \, \Delta p^n \tag{4.6} \end{equation}\]

Avec \(n\) un exposant donc la valeur se siture entre 0.5 et 1.

Sur la base de cette équation, on peut calculer deux indicateurs :

• \(Q_{4Pa,surf}\) en m\(^3\)/h/m\(^2\) est le débit obtenu pour \(\Delta p=4\) Pa, divisé par la surface déperditive du bâtiment;
• \(n50\) en vol/h est le taux de renouvellement obtenu pour \(\Delta p=50\) Pa.

La RE2020 impose les valeurs maximales suivantes pour \(Q_{4Pa,surf}\) selon l’usage du bâtiment

Usage	Valeur max \(Q_{4Pa,surf}\)
Maison individuelle	0.6
Logements collectifs	1
Bâtimetns tertiaires	1.6
Autres usages	3.0

4.3 Ventilation naturelle

La ventilation naturelle est le déplacement d’air qui n’est pas dû à une ventilation mécanique contrôlée. Elle provient de deux forces principales qui génèrent des variations locales de pression, qui ensuite résultent en un déplacement d’air des zones de pression élevée vers les pressions faibles : le vent et le tirage thermique.

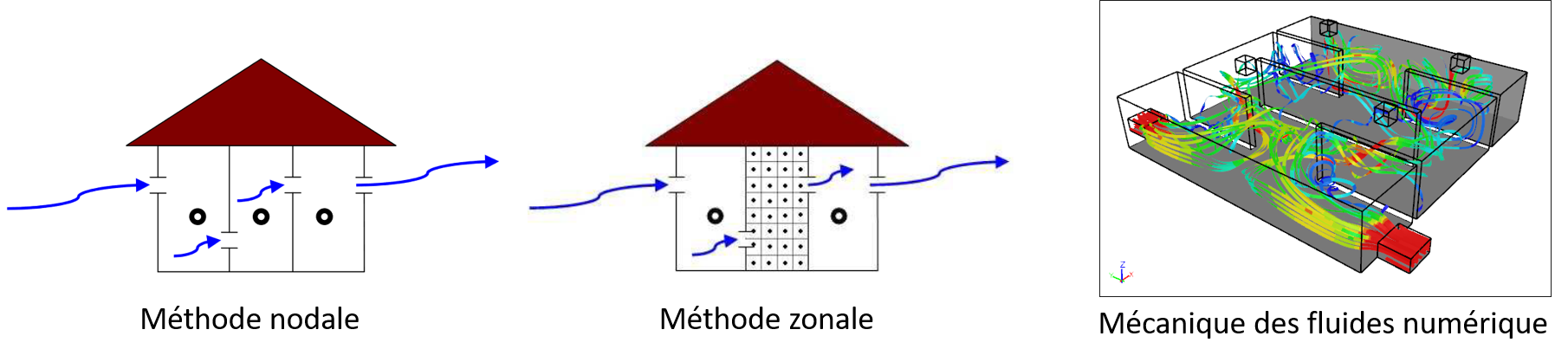
Figure 4.4: Trois modes de modélisation aéraulique

• La méthode nodale, ou airflow network, où on considère les variables (température, pression, masse volumique) comme uniformes dans chaque zone.
• La méthode zonale, où une zone peut être divisée en sous-volumes pour représenter l’hétérogénéité de ces variables dans une même pièce.
• La mécanique des fluides numérique qui modélise les écoulements par les équations de Navier-Stokes sur un maillage fin des volumes.

4.3.1 Méthode nodale

La méthode nodale peut être comparée à l’analogie électrique utilisée pour les transferts thermiques : chaque zone est représentée par un noeud de pression. Ceux-ci sont reliés par des résistances représentant les chemins que peuvent prendre les écoulements d’air : entrées d’air, fenêtres, fissures… Un ventilateur crée une différence de pression qui mettra l’air en mouvement dans le reste du réseau.

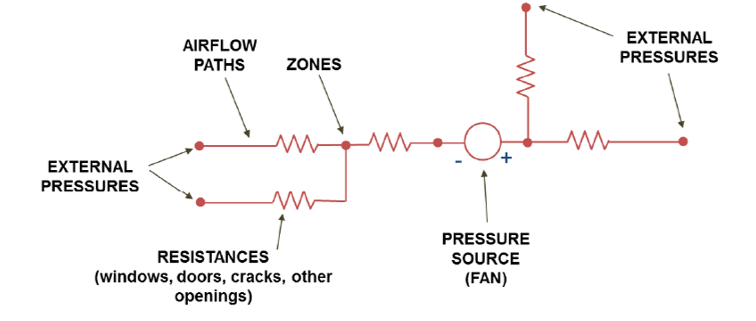
Figure 4.5: Principe de la méthode nodale : les chemins de l’air sont des résistances qui relient les noeuds de pression

Le plus souvent, le calcul des transferts aérauliques dans un bâtiment se fait sous les hypothèses qui permettent d’utiliser le théorème de Bernoulli : fluide parfait incompressible en régime stationnaire et isotherme. Ce théorème énonce la conservation de la quantité suivante en tous points le long d’une ligne de courant : \[\begin{equation} \frac{1}{2}\, \rho \, v^2+P+\rho \, g \, z = \mathrm{constant} \tag{4.7} \end{equation}\] où \(P\) est la pression, \(\rho\) la masse volumique, \(v\) la vitesse de l’air et \(z\) la hauteur.

Le deuxième théorème principal est la loi des gaz parfaits qui relie la pression, la masse volumique et la température : \[\begin{equation} P = \rho \, R_a \, T \tag{4.8} \end{equation}\] où \(R_a \approx 287\) J.kg\(^{-1}\).K\(^{-1}\) est la constante spécifique de l’air, soit le rapport entre la constante universelle des gaz parfaits et la masse molaire de l’air.

Le premier type d’équations nécessaires pour appliquer la méthode nodale est la relation entre la pression de part et d’autre d’une ouverture et le débit d’air qui la traverse. Sur un schéma comme la figure 4.5, ce serait le rapport entre les intensités (débit d’air) et les potentiels (pressions).

L’écoulement à travers une très petite ouverture (infiltrations dans des fissures) peut être décrit par : \[\begin{equation} Q = K \cdot \left|\Delta P\right|^n \tag{4.9} \end{equation}\] où \(Q\) est le débit volumique, le coefficient \(K\) caractérise l’ouverture, \(n\) est un exposant proche de \(1/2\), et \(\Delta P\) est l’écart de pression de part et d’autre de l’ouverture.

L’écoulement \(Q\) à travers une ouverture un peu plus importante (entrées d’air, détalonnage d’une porte) se décrit par : \[\begin{equation} Q = A^* \sqrt{\frac{2\cdot|\Delta P|}{\rho}} \tag{4.10} \end{equation}\] où \(A^*\) est la surface effective de l’ouverture, qui dépend de son ouverture \(A\) et d’un coefficient de décharge \(C_d\) : \[\begin{equation} A^*=A\cdot C_d \tag{4.11} \end{equation}\]

Le coefficient de décharge \(C_d\) peut être proche de 1 pour une ouverture importante et un écoulement laminaire, mais est inférieur à 1 la plupart du temps. Lorsque l’air circule de part et d’autre d’une pièce à travers deux ouvertures, alors la surface effective de ce “parcours” de l’air peut s’exprimer en fonction des propriétés de chacune des deux ouvertures : \[\begin{equation} A^* = \frac{1}{\sqrt{ \left(\frac{1}{C_{d1}\cdot A_1}\right)^2 +\left(\frac{1}{C_{d2}\cdot A_2}\right)^2 }} \tag{4.12} \end{equation}\]

4.3.2 Vent

Le vent entraîne une hausse ou une baisse de la pression en façade d’un bâtiment. Cette variation \(\Delta P\) dépend d’un coefficient de pression \(C_p\) et de la vitesse du vent \(V_\mathit{vent}\) :

\[\begin{equation} \Delta P = \frac{1}{2} \, \rho \, C_p \, V_\mathit{vent}^2 \tag{4.13} \end{equation}\]

Le coefficient de pression est une valeur empirique déterminée par la géométrie du bâtiment et son orientation par rapport à la direction du vent. Sa valeur sera positive sur une façade exposée au vent : la pression de l’air au contact du mur est plus élevée que la pression atmosphérique. Au contraire, \(C_p\) est négatif sur une façade sous le vent, en dépression.

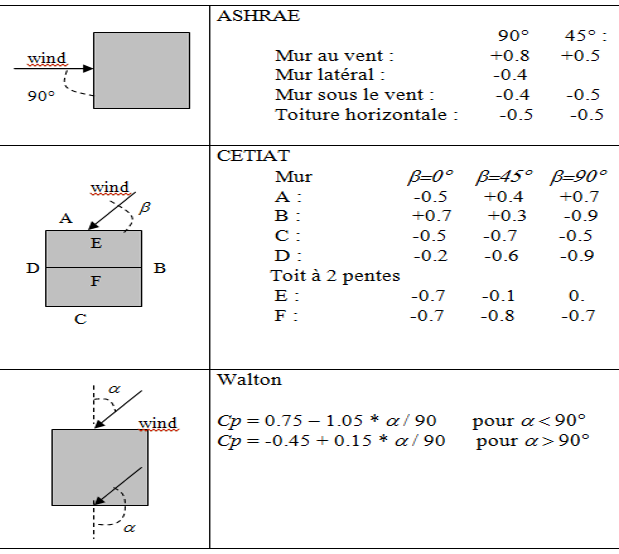
Figure 4.6: Coefficients de pression pour l’expression de l’influence du vent

On peut appliquer la méthode nodale pour calculer le débit d’air induit par le vent dans un bâtiment, à partir des équations (4.9) et (4.13). Si on suppose un local doté de deux ouvertures, chacune avec un coefficient de pression \(C_{p1}\) et \(C_{p2}\) respectivement :

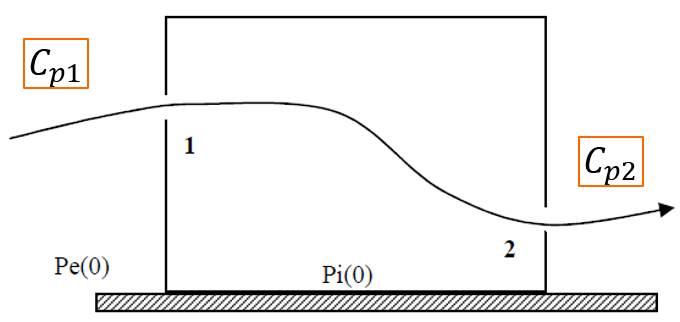
Figure 4.7: Débit d’air induit par le vent, calculé par la méthode nodale

On peut alors démontrer (une démonstration complète est donnée dans la vidéo plus bas) que le débit d’air traversant le bâtiment sous l’effet d’un vent de vitesse \(V_\mathit{vent}\) (m/s) est :

\[\begin{equation} Q = A^* V_\mathit{vent} \sqrt{\Delta C_p} \tag{4.14} \end{equation}\]

où \(A^*\) est la surface effective des ouvertures définie par l’équation (4.12). Le débit d’air est d’autant plus fort que la différence entre les deux coefficients de pression est importante : c’est le cas par exemple d’une ventilation traversante dans l’axe du vent. Au contraire, deux ouvertures situées sur la même façade auront des \(C_p\) très proches donc une ventilation naturelle par le vent plus faible.

4.3.3 Tirage thermique

Le tirage thermique est la conséquence d’une différence de température entre l’air intérieur et extérieur. Celle-ci entraîne un écart de leur masse volumique du fait de la loi des gaz parfaits (équation (4.8)) : \(\rho \propto 1/T\)

Le théorème de Bernoulli (équation (4.7)) indique que la pression de l’air décroît avec l’altitude, proportionnellement à la masse volumique. La pression à une hauteur \(z\) est inférieure à celle au niveau 0 (on suppose ici l’absence de vent) :

\[\begin{equation} P(z) = P(0) - \rho g z \tag{4.15} \end{equation}\]

La décroissance de pression \(\rho g z\) est proportionnelle à \(\rho\), donc inversement proportionnelle à la température : dans un milieu froid, la pression décroît plus vite avec l’altitude que dans un milieu chaud.

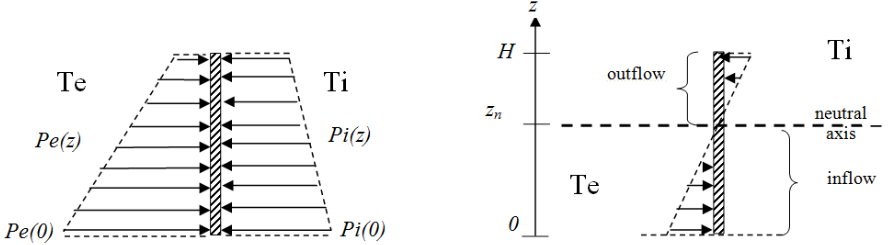
Figure 4.8: Tirage thermique

On se place dans l’exemple montré sur la figure 4.8 de deux milieux séparés, aux températures \(T_e\) et \(T_i\), avec par exemple \(T_e < T_i\). A une altitude fixée \(z\), la différence de pression entre l’extérieur et l’intérieur est :

\[\begin{align} P_e(z) - P_i(z) & = \left( P_e(0)-\rho_e \, g \, z\right) - \left( P_i(0)-\rho_i \, g \, z \right) \\ & = \left[ P_e(0)-P_i(0) \right] -\rho_e \, g \, z \, \frac{T_i-T_e}{T_i} \tag{4.16} \end{align}\]

Si \(P_e(0)>P_i(0)\) il existe donc une coordonnée à laquelle le rapport des pressions s’inverse. On appelle axe neutre \(z_n\) cette hauteur où les pressions intérieure et extérieure sont égales : \[\begin{equation} z_n = \frac{P_e(0)-P_i(0)}{g(\rho_i-\rho_e)} \tag{4.17} \end{equation}\]

Donc dans l’exemple d’une température extérieure inférieure à la température intérieure, l’effet du tirage thermique est que:

• en dessous de l’axe neutre \(z_n\), \(P_e > P_i\) donc l’air rentre dans le bâtiment,
• au dessus de l’axe neutre, \(P_e < P_i\) donc l’air sort du bâtiment.

Cette variation de l’écart de pression entraîne un déplacement d’air de haut en bas dans le bâtiment, d’où le nom de tirage thermique.

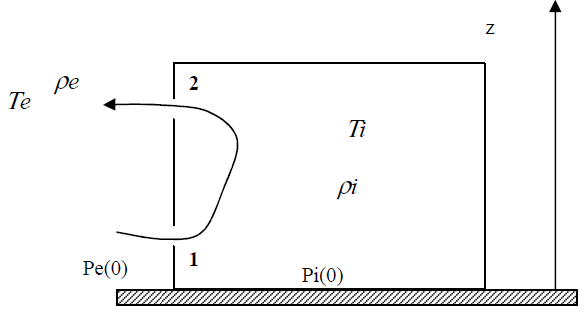
Figure 4.9: Débit induit par le tirage thermique à travers deux ouvertures

Lorsqu’un bâtiment possède deux ouvertures séparées par une hauteur \(H\), on peut démontrer (une démonstration complète est donnée dans la vidéo plus bas) que le débit d’air traversant le bâtiment sous l’effet du tirage thermique est :

\[\begin{equation} Q = A^* \sqrt{2 \, g \, H\frac{T_i-T_e}{T_i}} \tag{4.18} \end{equation}\]

4.3.4 Bilan

Si on inclut l’effet du vent et du tirage thermique dans les équations du modèle aéraulique nodal, on peut exprimer le débit d’air traversant un bâtiment sous l’effet de la ventilation naturelle. Deux exemples sont donnés dans cette vidéo :

Dans les deux paragraphes ci-dessus, on a donné les formules des débits d’air traversant un bâtiment possédant deux ouvertures, sous l’effet soit du vent, soit du tirage thermique. Ces deux effets peuvent cependant se cumuler ou s’opposer. La somme des équations (4.14) et (4.18) est alors : \[\begin{equation} Q=A^* \left( \sqrt{\left|\Delta C_p\right|\cdot V_\mathit{vent}^2 } \pm \sqrt{2\cdot g\cdot H \left(\frac{|\Delta T|}{\bar{T}}\right) } \right) \tag{4.19} \end{equation}\] où \(\bar{T}\) est la moyenne de température entre intérieur et extérieur en Kelvin. Le signe \(\pm\) de cette formule vient du faire que l’effet du vent et du tirage thermique sont soit dans le même sens et s’additionnent, soit de sens opposés.

4.4 Exercices

4.4.1 Exercice 1 : vent et tirage thermique

Le bâtiment montré sur la figure 4.10 a deux ouvertures opposées, en partie basse et en partie haute, séparées par une différence d’altitude \(\Delta z\). Le vent souffle dans la direction montrée sur la figure. La température intérieure est 20°C, température extérieure 0°C. Les coefficients de pression des deux ouvertures sont 0,6 et -0,4 respectivement.

Figure 4.10: Vent et tirage thermique dans un bâtiment

1. Quelle est la direction du débit d’air induit par le tirage thermique ? Cette force est-elle opposée au vent ?
2. La vitesse du vent est 5 m/s et la hauteur \(\Delta z\) est 10 m. En utilisant l’équation (4.19), trouver quelle force l’emporte sur l’autre et dans quel sens l’air circule dans le bâtiment.
3. Pour quelle valeur de la vitesse du vent les deux forces s’annulent-elles ?

4.4.2 Exercice 2 : cheminée solaire

On étudie la cheminée solaire montrée sur la figure 4.11. L’air est chauffé dans la cheminée, créant un effet de tirage thermique vers le haut. L’air est mis en dépression dans le bâtiment, ce qui attire l’air extérieur à travers un puits canadien. On cherche à calculer la température intérieure du bâtiment sous l’effet de cet apport d’air frais.

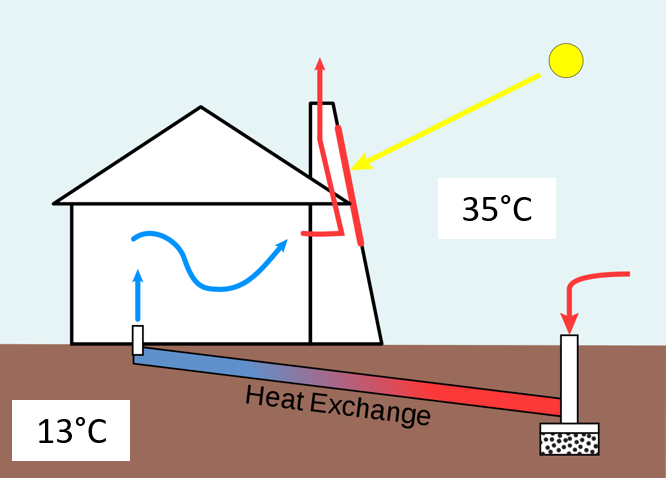
Figure 4.11: Cheminée solaire

Dans la cheminée, l’air circule entre une paroi de verre et un mur de béton. On ne donne pas ici de valeur numérique pour chaque variable, mais elles pourront être prises de manière réaliste pour voir la conséquence sur les résultats du calcul.

Pour résoudre le problème, on a besoin de trois équations :

1. Ecrire le bilan thermique de la maison en fonction de son coefficient global de déperditions \(D=100\) W/K et du débit d’air \(\dot{m}\).
2. Formuler le débit d’air \(\dot{m}\) en fonction de la température de l’air en entrée \(T_i\) et à la sortie de la cheminée \(T_\mathrm{out}\), et de la différence d’élévation \(z\) entre ces deux points.
3. Ecrire un bilan thermique à l’intérieur de la cheminée pour estimer la température maximale de l’air qui en sort.

Solution

1. En notant \(T_\mathrm{in}\) la température d’entrée de l’air, \(T_i\) et \(T_e\) les températures intérieure et extérieure : \[\begin{equation} \dot{m} c_p \left(T_\mathrm{in}-T_i\right) + D \left(T_e-T_i\right) = 0 \tag{4.20} \end{equation}\]

2. On reprend la formule (4.18) du tirage thermique en considérant que la température “intérieure” à la cheminée est \(T_\mathrm{out}\) et la température “extérieure” est celle de l’air entrant, soit \(T_i\): \[\begin{equation} Q = A^* \sqrt{2 \, g \, z\frac{T_\mathrm{out}-T_i}{T_\mathrm{out}}} \tag{4.21} \end{equation}\] où \(A^*\) est la surface effective des ouvertures de la cheminée et \(Q=\dot{m}/\rho\) est le débit volumique à la sortie.

3. L’air dans la cheminée est situé entre une paroi vitrée et une paroi isolée qui absorbe une partie du rayonnement solaire. Le calcul de sa température se fait par la même méthode que dans l’exemple de la serre, exercice 5.4.1.