Chapitre 7 Humidité

L’humidité dans les bâtiments peut provenir des activités des occupants (cuisine, salle de bain, lessives…), d’infiltration d’eau de pluie dans la façade, ou bien de remontées capillaires depuis le sol. Si les mesures nécessaires ne sont pas prises, elle peut s’accumuler dans l’air, ce qui peut poser des problèmes d’hygiène, ou dans les matériaux, pouvant compromettre leur durabilité et leurs performances.

7.1 Air humide

Résumé en vidéo :

Pour comprendre les problématiques d’humidité dans les bâtiments, on commence par une description de l’air humide. Celui-ci est considéré comme un mélange de deux gaz : l’air sec et la vapeur d’eau. Ses propriétés sont affichées sur le diagramme de l’air humide, ou diagramme psychrométrique.

Figure 7.1: Diagramme de l’air humide

Un état donné de l’air, en termes de température et d’humidité, est représenté par un point sur le diagramme. Celui-ci permet alors de lire toutes ses propriétés, au nombre de 7 :

La température d’air sec \(T\), ou plus simplement la température tout court.
L’humidité relative HR est le rapport entre la pression partielle de vapeur dans l’air \(p_\mathit{vap}\), et la pression de vapeur saturante \(p_\mathit{sat}\). Cette dernière est la pression maximale qui pourrait être atteinte par la vapeur à une température donnée. \[\begin{align} \mathrm{RH} & = \frac{p_\mathit{vap}}{p_\mathit{sat}} \tag{7.1} \\ p_\mathit{sat}(T) & = \mathrm{exp} \left(23.5771-\frac{4042.9}{T+273.15-37.58}\right) \tag{7.2} \end{align}\]
La teneur en eau \(w\), ou humidité absolue, ou rapport de mélange, est la quantité d’eau (en masse) par unité de masse d’air sec. Son unité est [kg\(_\mathit{vap}\)/kg\(_\mathit{as}\)] (à partir d’ici, l’indice “vap” désigne la vapeur d’eau et l’indice “as” désigne l’air sec). \[\begin{equation} w = \frac{\rho_\mathit{vap}}{\rho_\mathit{as}} = \frac{r_\mathit{as}}{r_\mathit{vap}} \frac{p_\mathit{vap}}{p_\mathit{atm}-p_\mathit{vap}} \tag{7.3} \end{equation}\] où \(r_\mathit{as}\) et \(r_\mathit{vap}\) désignent les constantes thermodynamiques de l’air sec et de la vapeur d’eau (valeurs données plus bas), et \(p_\mathit{atm}\) est la pression atmosphérique.
L’enthalpie spécifique \(h\) est l’énergie interne totale du mélange d’air sec et de vapeur d’eau, par unité de masse d’air sec. C’est la somme de la chaleur sensible et de la chaleur latente \[\begin{equation} h = c_\mathit{as}\, T + w \, (l_v+c_\mathit{vap}\, T) \tag{7.4} \end{equation}\] où \(c_\mathit{as}\) est la chaleur spécifique de l’air sec, \(c_\mathit{vap}\) celle de la vapeur d’eau, et \(l_v\) sa chaleur latente de vaporisation (valeurs données plus bas).
Le volume spécifique \(v_s\) est le volume occupé par le mélange, par unité de masse d’air sec, en m\(^3\)/kg\(_{as}\). C’est l’inverse de la masse volumique de l’air sec \(\rho_\mathit{as}\). \[\begin{equation} \rho_\mathit{as} = \frac{1}{v_s} = \frac{p_\mathit{atm}}{\left(w \, r_\mathit{vap}+r_\mathit{as}\right) T} \tag{7.5} \end{equation}\]
La température d’air humide \(T_{ah}\) est la température qu’aurait l’air s’il était saturé en humidité à enthalpie constante.
La température de rosée \(T_r\) est la température qu’aurait l’air s’il était saturé en humidité à teneur en eau constante.

Table 7.1: Constantes de l’air humide
Variable	Air sec (as)	Vapeur d’eau (vap)
Chaleur spécifique \(c_p\) [J.kg\(^{-1}\).K\(^{-1}\)]	1000	1850
Constante thermo. \(r\) [J.kg\(^{-1}\).K\(^{-1}\)]	287	462
Chaleur latente d’évap. \(l_v\) [J.kg\(^{-1}\)]	.	\(2.5 \times 10^6\)

Toutes les formules ci-dessus peuvent être remplacées par la lecture du diagramme. Il suffit de connaître deux des sept propriétés pour en déduire les autres, soit par lecture, soit par calcul.

Le diagramme de l’air humide est utile pour estimer le risque de condensation dans un matériau. Cela peut arriver par exemple dans une pièce humide mal isolée : si la température en surface de la paroi descend sous la température de rosée, qui dépend uniquement de la teneur en eau, alors on voit l’apparition de condensation. On parle aussi de point de rosée.

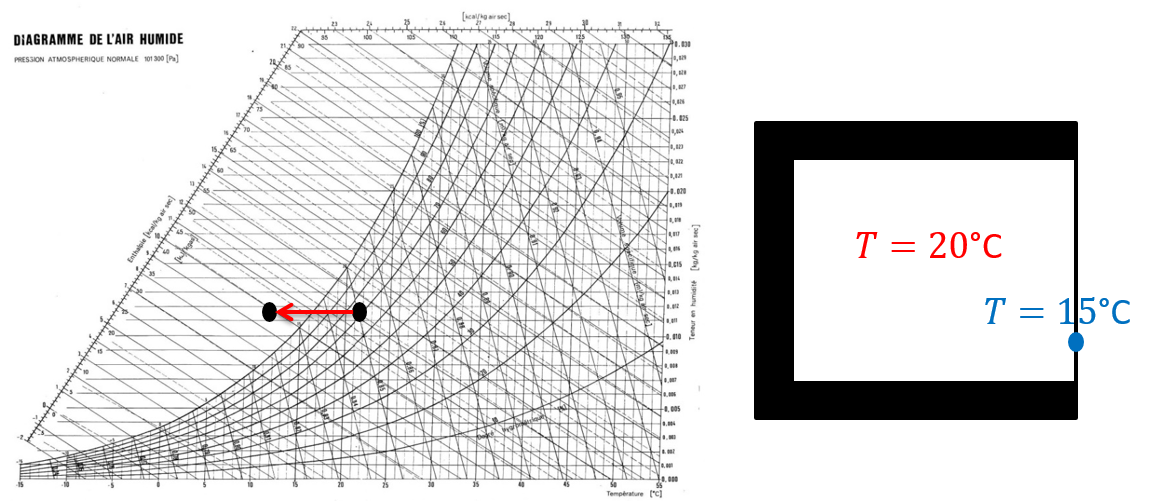
Figure 7.2: Risque de condensation si la température descend sous le point de rosée

On donne ici l’exemple montré sur la figure 7.2 d’une pièce à 20°C et humidité relative 80%. On suppose qu’une fenêtre est 15°C du fait de son contact avec l’air extérieur.

La pression de vapeur saturante de l’air est \(p_\mathit{sat}(20°)=2340\) Pa (formule (7.2))
La pression de vapeur saturante au contact de la vitre est \(p_\mathit{sat}(15°)=1707\) Pa.
La pression partielle de vapeur dans l’air est \(p_\mathit{vap}=\mathrm{HR} \cdot p_\mathit{sat}(20°) = 1872\) Pa

De la buée apparaît sur la vitre car la pression de vapeur dans l’air est supérieure à la pression saturante au contact de la vitre.

7.2 Humidité dans les matériaux

L’humidité peut migrer à travers les matériaux par diffusion de la vapeur, ou par capillarité de l’eau liquide. La plupart des matériaux ont une certaine capacité d’accumuler l’humidité par adsorption. Afin d’empêcher l’apparition de points de rosée ou l’accumulation d’eau à l’intérieur d’une paroi, il est important de bien choisir sa configuration : position de l’isolant, présence de pare-vapeur ou non, enduit, etc. L’exercice 2 ci-dessous va illustrer cette question.

La modélisation des transferts d’humidité dans les matériaux suit une équation similaire à celle des transferts thermiques.

\[\begin{equation} \frac{\partial w}{\partial t} = -\mathrm{div} \left( g_\mathrm{vap} + g_\mathrm{liq} \right) \tag{7.6} \end{equation}\]

où \(g_\mathrm{vap}\) et \(g_\mathrm{liq}\), en [kg.s\(^{-1}\).m\(^{-2}\)] désignent les débits surfaciques d’eau vapeur et liquide à l’intérieur du matériau. La teneur en eau \(w\) est exprimée ici en [kg.m\(^{-3}\)], mais peut être ramenée en kg/kg comme celle définie dans l’équation (7.3) pour l’air d’une pièce.

Dans la suite, on va négliger le transfert d’eau à l’état liquide, qui arrive surtout lors d’infiltrations importantes d’eau de pluie ou de remontées capillaires.

La diffusion de vapeur suit la loi de Fick, équivalente à la loi de Fourier pour la conduction thermique : le flux est induit par un gradient de pression de vapeur de part et d’autre d’un milieu poreux de perméabilité \(\delta_\mathrm{vap}\).

\[\begin{equation} g_\mathrm{vap} = - \delta_\mathrm{vap} \nabla p_v \tag{7.7} \end{equation}\]

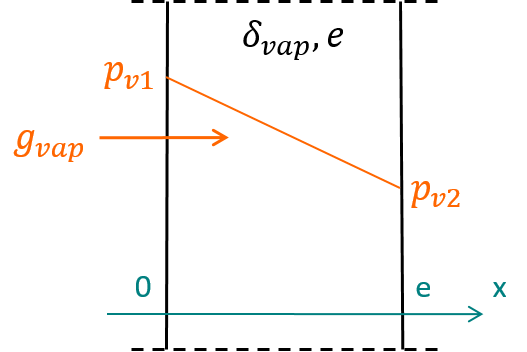
Figure 7.3: Diffusion de vapeur dans un mur à l’état stationnaire

On peut donc démontrer que la distribution de la pression de vapeur de part et d’autre d’une paroi est linéaire à l’état stationnaire, comme montré sur la figure 7.3.

\[\begin{equation} g_\mathrm{vap} = \frac{\delta_\mathrm{vap}}{e}(p_{v1}-p_{v2}) \tag{7.8} \end{equation}\]

Comme on l’a fait pour la conduction thermique stationnaire 1D (chapitre 3.1), on peut donc définir une résistance de transfert d’humidité \(R=e/\delta_\mathrm{vap}\), similaire à la résistance thermique. Enfin, l’échange de vapeur entre la surface d’un mur et l’air peut également être formulé par un coefficient de transfert surfacique \(h_m\) :

\[\begin{equation} g_\mathrm{vap} = h_m (p_{v,\mathrm{surf}}-p_{v,\mathrm{air}}) \tag{7.9} \end{equation}\]

On peut utiliser les équations (7.8) et (7.9) pour calculer la distribution de la pression de vapeur à travers un mur multicouche, avec une analogie électrique, comme on l’a fait avec les températures. L’analogie entre les variables du transfert thermique et du transfert massique est montré par le tableau ci-dessous :

Table 7.2: Equivalence entre transfert de chaleur et d’humidité
Type	Chaleur	Humidité
Flux	\(\phi\) (W.m\(^{-2}\))	\(g_\mathrm{vap}\) (kg.s\(^{-1}\).m\(^{-2}\))
Potentiel	\(T\) (K)	\(p_v\) (Pa)
Résistance	\(e/\lambda\) (m\(^{2}\).K.W\(^{-1}\))	\(e/\delta_\mathrm{vap}\) (m.s\(^{-1}\))
Capacité	\(c_p\) (J.kg\(^{-1}\).K\(^{-1}\))	\(\partial w/\partial p_v\)

7.3 Bilans d’humidité

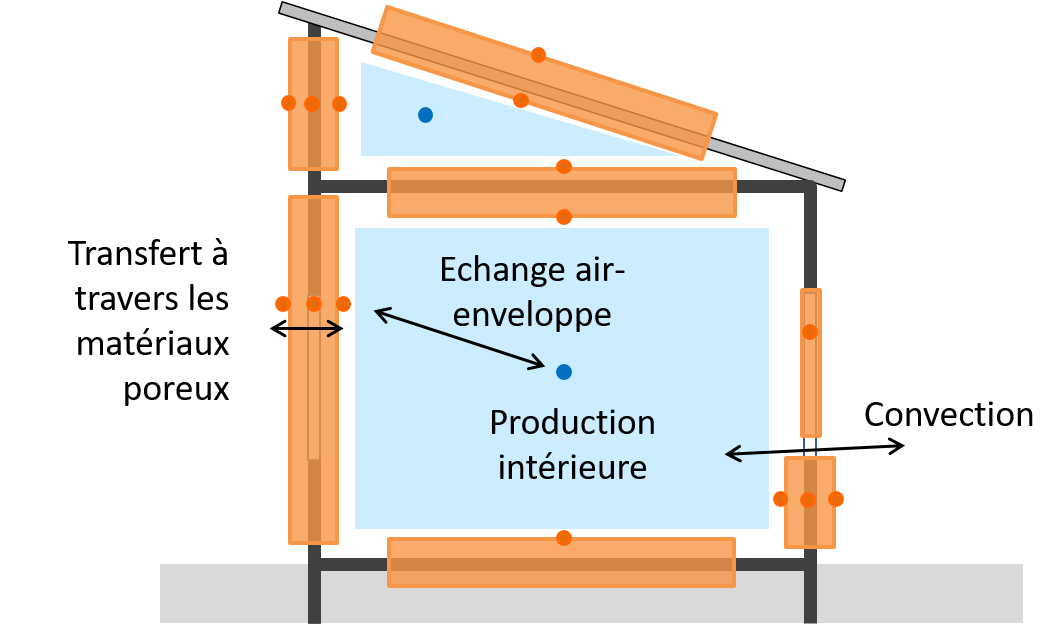
Figure 7.4: Bilan d’humidité à l’échelle d’un local

Comme on l’a fait pour les transferts thermiques, on peut faire le bilan des transferts d’humidité dans un bâtiment avec la loi de conservation de la masse.

\[\begin{equation} \frac{\mathrm{d}M_{H_2O}}{\mathrm{d}t} = G_{H_2O,\mathrm{produit}} + G_{H_2O,\mathrm{entrant}} - G_{H_2O, \mathrm{sortant}} \end{equation}\]

\(M_{H_2O}\) (kg) est la quantité d’eau dans un certain volume d’air ;
\(G_{H_2O,\mathrm{produit}}\) (kg/s) est la production intérieure d’humidité par les activités des occupants ;
\(G_{H_2O,\mathrm{entrant}}\) et \(G_{H_2O, \mathrm{sortant}}\) (kg/s) sont les quantités de vapeur d’eau entrant et sortant de la pièce, par échange avec les matériaux poreux de l’enveloppe, ou par convection dans l’air échangé avec les autres pièces.

Une pièce de volume \(V\) et dont l’air a une teneur en eau \(w\) contient une quantité totale de vapeur d’eau :

\[\begin{equation} M_{H_2O}=\rho_a \cdot V \cdot w \end{equation}\]

On peut exprimer l’échange d’humidité entre l’air et les matériaux par les formules de la section précédente, ou par des modèles plus simples. L’échange d’humidité entre deux pièces est plus simple : un débit d’air \(\dot{m}\) entre deux pièces dont les teneurs en eau sont \(w_1\) et \(w_2\) transporte une quantité d’eau \(G=\dot{m}(w_1-w_2)\).

7.4 Exercices

7.4.1 Exercice 1 : condensation

Une fenêtre sépare une pièce à \(T=20\)°C de l’extérieur à \(T_e=8\)°C. La fenêtre a une épaisseur de 4 mm et une conductivité thermique de 1.1 W.m\({-1}\).K\(^{-1}\). Les résistances de transfert surfacique sont 0.13 et 0.04 m\(^2\).K.W\(^{-1}\), respectivement.

Calculer la température de surface intérieure de la fenêtre.
Calculer la pression de vapeur saturante dans la pièce et à la surface de la fenêtre
A partir de quelle humidité relative dans la pièce voit-on apparaître de la buée sur la fenêtre ?

Solution

11.1 °C
2340 Pa et 1322.4 Pa
56 %

7.4.2 Exercice 2 : point de rosée

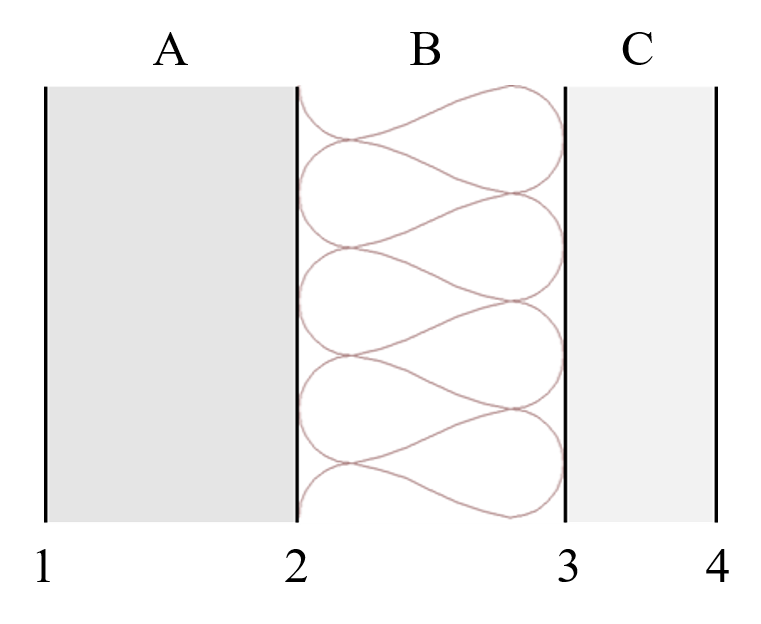
Figure 7.5: Mur multicouche : y a-t-il de la condensation ?

Le mur montré sur la figure 7.5 a trois couches. L’épaisseur, la conductivité thermique et la perméabilité vapeur de chaque couche sont données dans le tableau suivant, ainsi que les coefficients de transfert surfaciques pour la chaleur et l’humidité.

Table 7.3: Propriétés des matériaux
Materiau	Epaisseur (m)	\(\lambda\) [W.m\(^{-1}.\)K\(^{-1}\)]	\(\delta_\mathrm{vap}\) [s]
Béton	0.18	2	\(2.2\times 10^{-12}\)
Isolant	0.15	0.04	\(1.5\times 10^{-10}\)
Placo	0.013	0.35	\(9\times 10^{-12}\)

Table 7.4: Coefficients de transfert surfaciques
Côté	\(h_t\) [W.m\(^{-2}.\)K\(^{-1}\)]	\(h_m\) [s.m\(^{-1}\)]
Extérieur	16	\(4\times10^{-8}\)
Intérieur	4.1	\(1\times10^{-8}\)

Conditions intérieures : \(T_i=20\)°C et HR\(_i\)=60\(\%\).
Conditions extérieures : \(T_e=6\)°C et HR\(_e\)=80\(\%\).

Calculer la pression de vapeur \(p_v\) de l’air intérieur et extérieur.
Calculer la température, pression de vapeur saturante, et pression de vapeur à chaque interface entre les matériaux (les 4 points montrés sur la figure 7.5).
Est-ce qu’il y a un point de rosée quelque part ?