Chapitre 5 Rayonnement

5.1 Principes de rayonnement

Le chapitre 3 a traité les transferts thermiques à travers les parois, entre les parois et l’air, et entre les différents volumes d’air. Un dernier type de transfert doit être abordé : les échanges radiatifs entre les parois.

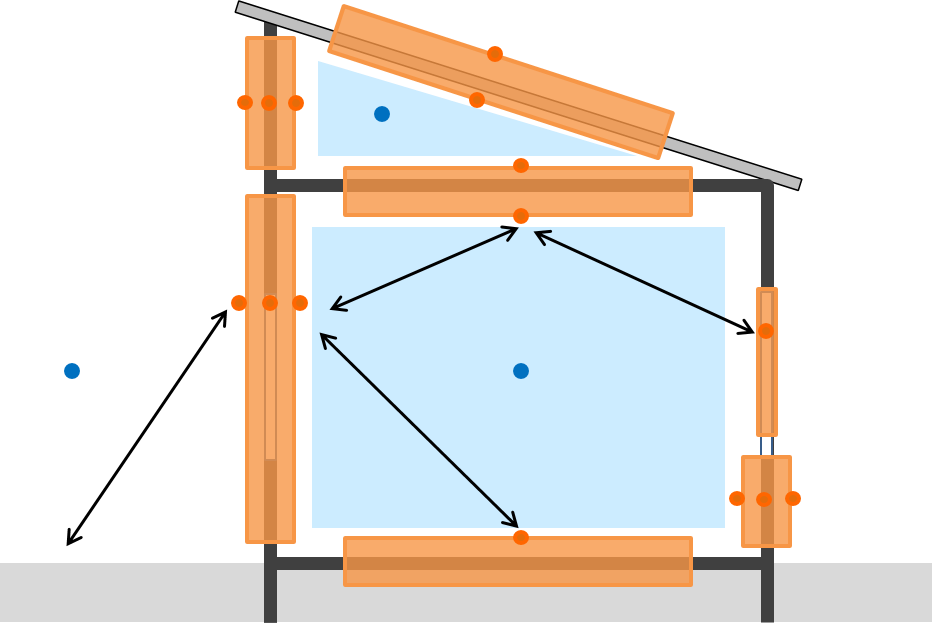
Figure 5.1: Interactions entre les températures des surfaces

La température de surface des murs, à l’intérieur ou à l’extérieur, est généralement différente de la température de l’air du fait de la résistance surfacique. En plus d’échanger de la chaleur par convection avec l’air, les parois en échangent entre elles par rayonnement, et en reçoivent d’autres sources : soleil, appareils de chauffage, occupants.

Figure 5.2: Rapport entre la température d’un corps noir et son spectre d’émission

La loi de Planck représentée sur la figure 5.2 décrit le spectre du rayonnement thermique émis par un corps noir en fonction de sa température. La longueur d’onde du maximum d’émission est inversement proportionnelle à la température. En thermique du bâtiment, on distingue donc deux types de rayonnement :

• le rayonnement solaire, principalement compris entre 300 et 2000 nm, qu’on appelle les courtes longueurs d’onde (CLO) ;
• le rayonnement émis par les bâtiments eux-mêmes et leur environnement, à des températures bien plus faibles donc de plus grandes longueurs d’onde (GLO) de plusieurs \(\mu\)m.

5.2 Apports solaires

Résumé en vidéo

La puissance radiative \(\Phi_\mathit{sol}\) (W) reçue par une surface d’absorptivité \(\alpha\) est la somme de l’ensoleillement direct \(E_\mathit{dir}\) (W.m\(^{-2}\)), l’ensoleillement diffus \(E_\mathit{dif}\) et celui réfléchi sur les surfaces voisines \(E_\mathit{ref}\) :

\[\begin{equation} \Phi_\mathit{sol} = \alpha \, S \, \left( E_\mathit{dir} + E_\mathit{dif} + E_\mathit{ref} \right) \tag{5.1} \end{equation}\]

Chacun de ces termes se calcule avec un peu de trigonométrie en fonction de la position du soleil par rapport à la paroi. Les variables nécessaires pour

• les données météorologiques mesurables : l’ensoleillement global et diffus horizontal, et la position du soleil (hauteur et azimut) ;
• l’orientation de la paroi : angle par rapport au sol, et azimut.

L’ensoleillement agit comme un apport thermique qui chauffe les surfaces exposées à l’intérieur ou à l’extérieur du bâtiment. Dans un calcul détaillé des transferts thermiques, il faut tenir compte de la position du soleil et de l’intensité du rayonnement à chaque heure de la journée. Dans le calcul réglementaire (très) simplifié, on utilise souvent des valeurs tabulées moyennes en fonction de la surface de vitrage sur chaque façade pour calculer les apports internes (voir l’exemple de l’exercice du chapitre 2).

Les apports thermiques dus au soleil dépendent en grande partie des caractéristiques des vitrages présents :

• la transmission lumineuse, la part de la lumière visible transmise par la vitre (environ 90% pour du vitrage simple, 70% pour du double vitrage à basse émissivité) ;
• le facteur solaire, le facteur de transmission de la partie infrarouge du rayonnement solaire, qui peut être diminué par le choix d’un vitrage sélectif pour limiter la surchauffe estivale ;
• le coefficient \(U\) de conductivité thermique, qui ne joue pas directement sur les transferts radiatifs.

5.3 Echanges radiatifs GLO

Le deuxième type de transfert radiatif de chaleur dans les bâtiments est celui à “grandes longueurs d’onde”, c’est-à-dire les échanges entre surfaces proches de la température ambiante. Ces transferts sont importants pour comprendre les apports de certains équipements de chauffage et la notion de confort thermique.

5.3.1 Définitions

Lorsqu’une surface reçoit un éclairement \(E\) (W.m\(^{-2}\)), ou densité de flux énergétique incident, cet éclairement est en partie absorbé, réfléchi et transmis. Les proportions de ces trois parties sont notées \(\alpha\), \(\rho\) et \(\tau\) respectivement, de sorte que

\[\begin{equation} \alpha + \rho + \tau = 1 \tag{5.2} \end{equation}\]

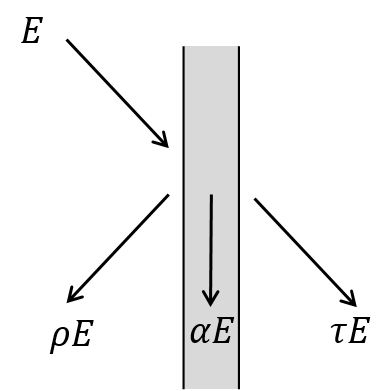
Figure 5.3: Répartition de l’éclairement reçu par une surface

D’autre part, une surface à la température \(T\) (K) émet un flux radiatif appelé émittance \(M\) par unité de surface (W.m\(^{-2}\)). Sous l’hypothèse d’un corps gris, sa valeur est liée à la température

\[\begin{equation} M = \varepsilon M^0 = \varepsilon \sigma T^4 \tag{5.3} \end{equation}\]

où \(\varepsilon\) est l’émissivité de la surface et \(\sigma = 5.67 \times 10^{-8}\) W.m\(^{-2}\).K\(^{-4}\) est la constante de Stefan-Boltzmann. \(M^0\) est l’émittance de corps noir, uniquement fonction de la température.

Le rayonnement thermique total émis par notre surface est donc la somme de deux termes: la part réfléchie de l’éclairement incident \(\rho E\), et son émissivité propre \(M\)

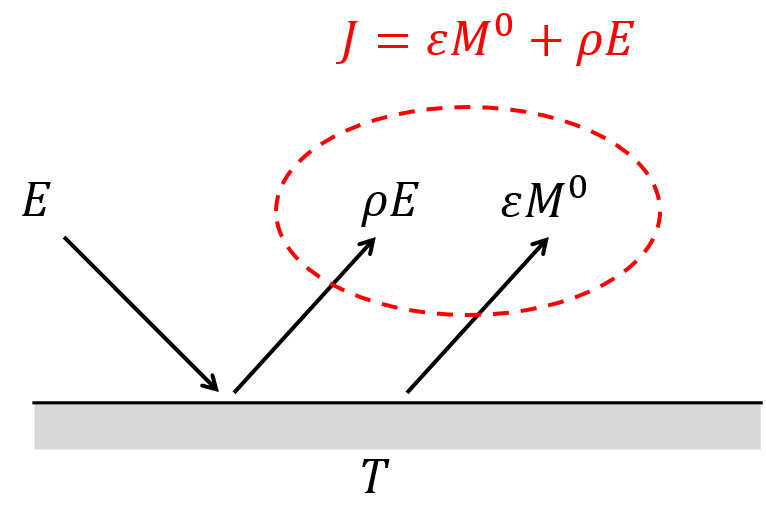
Figure 5.4: Flux total radiatif émis par une surface à une température donnée

On appelle radiosité \(J\) (W.m\(^{-2}\)) la somme de ces deux termes, c’est-à-dire le flux énergétique total quittant la surface par rayonnement.

\[\begin{equation} J = M + \rho \, E \tag{5.4} \end{equation}\]

Enfin, la dernière grandeur qu’on définit ici pour le calcul des bilans radiatifs est le flux net \(\Phi\) (W), qui est la différence entre le flux total incident et le flux total émis par la surface. Ce flux net peut être positif ou négatif, selon que la surface cède plus ou moins de chaleur qu’elle n’en reçoit de son environnement.

5.3.2 Résolution des bilans radiatifs

On considère maintenant l’échange radiatif entre plusieurs surfaces en vis-à-vis, par exemple les parois d’une pièce ou les façades de plusieurs bâtiments proches. Résoudre le bilan radiatif de ces surfaces revient à calculer leurs températures et leurs flux nets de chaleur sous l’effet du rayonnement thermique.

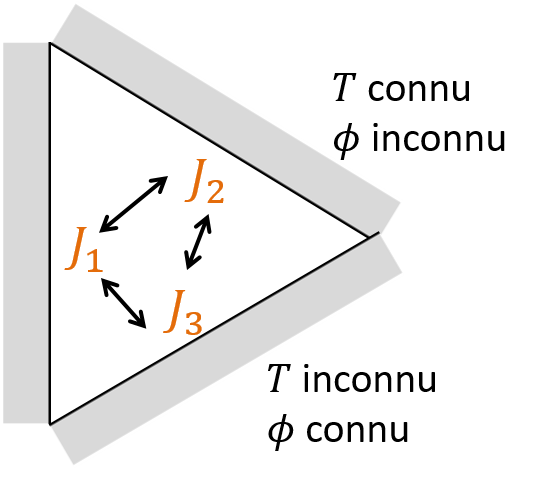
Figure 5.5: Echanges radiatifs entre plusieurs surfaces

Comme on a vu plus haut, le flux total (radiosité) émis par chaque surface dépend de son éclairement incident, issu des radiosités des autres surfaces avec lesquelles elle échange. Toutes les radiosités dépendent les unes des autres et il va falloir résoudre un système couplé.

Le système peut être résolu si chaque paroi a soit une température connue, soit un flux net de chaleur connu (par exemple une paroi adiabatique a un flux net nul). Pour chaque surface \(i\) du problème, on note \(T_i\), \(S_i\), \(J_i\) et \(\Phi_i\), sa température, surface, radiosité et flux net, et on écrit une des deux équations suivantes:

• Si sa température \(T_i\) est connue:

\[\begin{equation} J_i = \varepsilon_i \sigma T_i^4 + \rho_i \sum_{j=1}^n J_j F_{ij} \tag{5.5} \end{equation}\]

• Si son flux net \(\Phi_i\) est connu:

\[\begin{equation} \frac{\Phi_i}{S_i} = J_i - \sum_{j=1}^n J_j F_{ij} \tag{5.6} \end{equation}\]

En écrivant une équation pour chacune des \(n\) surfaces du problème, on obtient alors un système linéaire à \(n\) équations qui se résoud facilement pour déterminer toutes les radiosités. Une fois celles-ci connues, on peut en déduire les températures et flux nets inconnus des surfaces à partir de cette équation, qui est issue des deux précédentes:

\[\begin{equation} \frac{\Phi_i}{S_i} = \frac{\varepsilon_i}{1-\varepsilon_i} \left(\sigma T_i^4 - J_i\right) \tag{5.7} \end{equation}\]

On peut remarquer que les équations (5.5) et (5.6) contiennent des termes \(F_{ij}\) qu’on n’a pas encore spécifiés. Il s’agit des facteurs de forme entre les surfaces, qui seront expliqués dans la section suivante.

Pour finir, on peut évoquer un moyen simplifié de calculer l’échange radiatif \(\Phi_\mathit{rad}\) entre deux surfaces de températures connues \(T_1\) et \(T_2\) : la définition d’un coefficient de transfert radiatif \(h_r\).

\[\begin{align} \Phi_\mathit{rad} & = h_r \, S_1 \left(T_1 - T_2\right) \tag{5.8} \\ h_r & = \varepsilon \, F_{12} \sigma \left(T_1^2 + T_2^2\right)(T_1+T_2) \tag{5.9} \end{align}\]

5.3.3 Facteurs de forme

Le facteur de forme \(F_{ij}\) est la part du rayonnement thermique émis par la surface \(i\), reçu par la surface \(j\). C’est une donnée purement géométrique. Il correspond en quelque sorte à la question: “si un observateur se tient sur la surface \(i\), quelle est la part occupée par la surface \(j\) dans son champ de vision ?”

Tous les facteurs de forme sont des valeurs sans dimension comprises entre 0 et 1. On les détermine soit par des abaques, soit par des formules un peu compliquées comme dans cet exemple:

Figure 5.6: Facteurs de forme dans deux situations typiques

Une fois que certains facteurs de formes sont connus entre plusieurs surfaces, on peut généralement déduire les autres facilement avec les propriétés suivantes :

• Le principe de réciprocité :

\[\begin{equation} S_i F_{ij} = S_j F_{ji} \tag{5.10} \end{equation}\]

• La somme des facteurs de forme depuis une surface vaut 1 :

\[\begin{equation} \sum_{j=1}^n F_{ij} = 1 \tag{5.11} \end{equation}\]

5.3.4 Température radiative et opérative

La température radiative dans une pièce est la température d’un objet qui n’échangerait de la chaleur que par transfert radiatif avec les surfaces environnante, sans effets de conduction et de convection.

\[\begin{equation} T_r = \left(\sum_i F_i \varepsilon_i T_i^4 \right)^{1/4} \tag{5.12} \end{equation}\]

où \(F_i\) est le facteur de forme entre l’objet étudié et chacune des parois environnantes.

La température opérative décrit les effets combinés des transferts convectifs avec l’air, et des transferts radiatifs. Cette notion est utilisée pour la description du confort thermique.

\[\begin{equation} T_{op} = \frac{h_c T_a + h_r T_r}{h_c + h_r} \tag{5.13} \end{equation}\] où \(T_a\) est la température de l’air, \(h_c\) et \(h_r\) sont les coefficients d’échange convectif et radiatif.

5.4 Exercices

5.4.1 Exercice 1 : serre

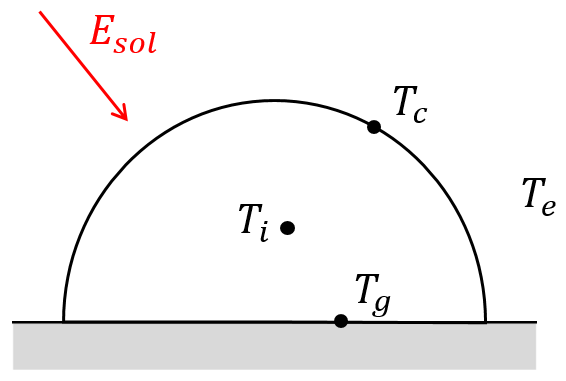
Figure 5.7: Exercice 1

Une serre est représentée par une demi-sphère montrée en figure 5.7. On suppose les hypothèses suivantes:

• Le diamètre de la serre est de 6 m.
• La température extérieure \(T_e\) est 24°C et l’ensoleillement \(E_\mathit{sol}\) est de 1000 W/m\(^2\). L’angle entre le soleil et le sol est de 60°.
• La couverture en verre est à la température \(T_c\). Elle a un coefficient de transmission solaire \(\tau_d = 0,8\) et une émissivité \(\varepsilon=0,95\) dans l’infrarouge. La résistance thermique du verre est très faible et peu être négligée.
• Les coefficients de transfert surfaciques sont: \(h_{gi}=2,6\) W/(m\(^2\).K) entre le sol et l’air intérieur ; \(h_{ci}=6,1\) W/(m\(^2\).K) entre la couverture et l’air intérieur ; \(h_{ce}=16\) W/(m\(^2\).K) entre la couverture et l’air extérieur.
• Le sol a une émissivité de 0.9. Il est considéré comme adiabatique : il n’y a pas de perte de chaleur vers le sous-sol.

Questions :

1. Calculer le facteur de forme \(F_{cg}\) entre la couverture et le sol. Grâce à la formulation simplifiée des échanges radiatifs (équations (5.8) et (5.9)), donner l’expression du coefficient de transfert radiatif \(h_r\) entre le sol et la couverture.
2. Dessiner le schéma des résistances thermiques entre toutes les températures : \(T_e\), \(T_c\), \(T_i\) et \(T_g\).
3. Ecrire le système de 3 équations dont les 3 inconnues sont : \(T_c\), \(T_i\) et \(T_g\).
4. Proposer une méthode de résolution du système, et évaluer ces trois températures.

5.4.2 Tutorial 2: radiateur

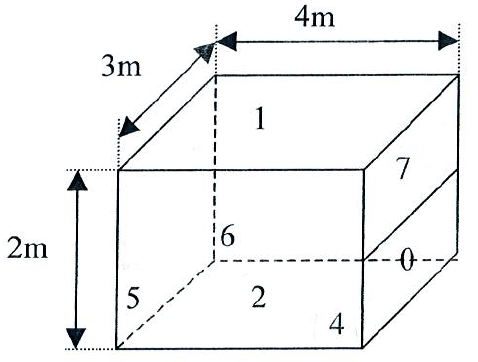
Figure 5.8: Exercice 2

On considère une pièce parallélépipédique aux dimensions montrées sur la figure 5.8.

• La surface \(S_5\) (mur vertical gauche) est une baie vitrée à la température \(T_5 = 8\)°C.
• La surface \(S_0\) est un radiateur couvrant la moitié de la hauteur du mur de droite, à la température \(T_0 = 60\)°C.
• La surface \(S_2\) (le sol) est adiabatique.
• Toutes les autres parois sont à la température \(T = 20°C\).

Calculer les pertes radiatives de la pièce par la fenêtre, le flux net radiatif cédé par le radiateur et la température du sol. L’émissivité de chaque surface est \(\varepsilon=0,85\) et la réflectivité est \(\rho=0,15\).

Solution

Toutes les parois à la température \(T = 20\)°C peuvent être considérées comme une seule surface, qu’on désignera avec l’indice 3. Le problème revient donc à un échange radiatif entre 4 surfaces: il faut écrire 4 équations.

Il faut d’abord trouver tous les facteurs de forme. On a besoin d’utiliser les formules de la figure 5.6 3 fois en tout, pour trouver les valeurs suivantes :

\(F_{25}=0,1174 \: ; \: F_{20}=0,081 \: ; \: F_{50}= 0,0477\)

Tous les autres facteurs de forme peuvent être déduits des formules simples: \(S_iF_{ij}=S_jF_{ji}\) et \(\sum_j F_{ij}=1\).

On écrit ensuite les 4 équations qui correspondant à chaque surface. Sur la surface 0 (le radiateur), la température est connue, ce qui donne :

\(J_0 =\varepsilon_0 \sigma T_0^4 + \rho_i\sum_{j=1}^n J_j F_{0j}\)

Sur la surface 2 (le sol), le flux net est connu : la surface est adiabatique donc \(\Phi_2=0\). On peut donc écrire l’équation:

\(0 = J_2 - \sum_{j=1}^n J_j F_{2j}\)

Les surfaces 3 et 5 ont le même type de condition aux limites que la surface 0 (température connue) donc leur équation est similaire. On aboutit finalement au système linéaire suivant dont la solution est un vecteur contenant les radiosités:

\[\begin{bmatrix} 1-\rho_0F_{00} & -\rho_0F_{02} & -\rho_0F_{03} & -\rho_0F_{05} \\ -F_{20} & 1-F_{22} & -F_{23} & -F_{25} \\ -\rho_3F_{30} & -\rho_3F_{32} & 1-\rho_3F_{33} & -\rho_3F_{35} \\ -\rho_5F_{50} & -\rho_5F_{52} & \rho_5F_{53} & 1-\rho_5F_{55} \end{bmatrix} \begin{bmatrix} J_0 \\ J_2 \\ J_3 \\ J_5 \end{bmatrix} = \begin{bmatrix} \varepsilon_0\sigma T_0^4 \\ 0 \\ \varepsilon_3\sigma T_3^4 \\ \varepsilon_5\sigma T_5^4 \end{bmatrix} \]

En résolvant ce système, on obtient les valeurs suivantes en W/m\(^2\) pour les radiosités:

\(J_0= 656,61 \: ; \: J_2=433,23 \: ; \: J_3 = 420,45 \: ; \: J_5=366,34\)

La dernière étape est d’utiliser la formule (5.7) pour trouver les valeurs demandées dans l’énoncé : la température du sol \(T_2\), le flux net du radiateur \(\Phi_0\) et le flux net sur la vitre \(\Phi_5\):

\(T_2= 22,5°C \: ; \: \Phi_0=711,53 W \: ; \: \Phi_5=-410,27 W\)